
Field X and Y are to be enclosed with fencing at the cost of $Rs.40$ per meter. If the cost on field X is denoted by ${C_X}$ and that on field Y is denoted by ${C_Y}$ , we have
(A) ${C_X} = {C_Y}$
(B) ${C_X} < {C_Y}$
(C) ${C_X} > {C_Y}$
(D) Cannot be determined

Answer
574.5k+ views
Hint:
Start with finding the perimeter of both the fields. The perimeter is the sum of the length of each side of the field. The perimeter of the square is four times its side. Find the perimeter of X and Y separately and multiply it with the rate of fencing for finding the total cost of fencing ${C_X}$ and ${C_Y}$ . Now check for the relationship between these two.
Complete Step by Step Solution:
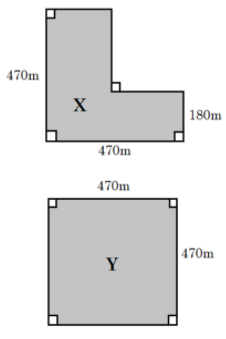
Here in this problem, we are given a diagram showing two fields X and Y with their dimensions. The cost of fencing these fields is $Rs.40$ per meter. The cost of field X and Y is given as ${C_X}$ and ${C_Y}$ . Now using this information we need to figure out which of the four given options is correct.
You must understand that the fencing will always be done exactly on the boundary of the field. Therefore, to find the total length of fencing required for both fields we must find out the perimeter of the fields. The perimeter of any two-dimensional polygon can be found by adding up the lengths of each side.
For field X, the total length of fencing $ = $ Sum of the lengths of all sides $ = $ Perimeter of X
$ \Rightarrow $ Perimeter of X $ = 470 + (180 + 290) + \left( {290 + 180} \right) + 470$
Now, these dimensions of sides of the field can be easily added as:
$ \Rightarrow $ Perimeter of X $ = 470 + 470 + 470 + 470 = 4 \times 470 = 1880{\text{m}}$
Similarly, for field Y, the total length of fencing $ = $ Sum of the lengths of all sides $ = $ Perimeter of Y
$ \Rightarrow $ Perimeter of Y $ = 470 + 470 + 470 + 470 = 4 \times 470 = 1880{\text{m}}$
For calculating the total cost of fencing be must multiply the perimeter with the rate off fencing, i.e. $Rs.40$ per meter
$ \Rightarrow $Cost of fencing X, i.e. ${C_X} = 1880 \times 40 = Rs.75200$
Similarly,
$ \Rightarrow $Cost of fencing Y, i.e. ${C_Y} = 1880 \times 40 = Rs.75200$
Therefore, we get ${C_X} = {C_Y}$
Hence, the option (A) is the correct answer.
Note:
In mensuration, the use of the fundamental concept of area and perimeter. An alternative approach to check for the relationship between ${C_X}$ and ${C_Y}$ can be taken by comparing the areas of the field X and Y. Since the rate of fencing is the same for both fields, the relation between the perimeter will be the same as the cost of fencing, i.e. ${C_X}$ and ${C_Y}$.
Start with finding the perimeter of both the fields. The perimeter is the sum of the length of each side of the field. The perimeter of the square is four times its side. Find the perimeter of X and Y separately and multiply it with the rate of fencing for finding the total cost of fencing ${C_X}$ and ${C_Y}$ . Now check for the relationship between these two.
Complete Step by Step Solution:
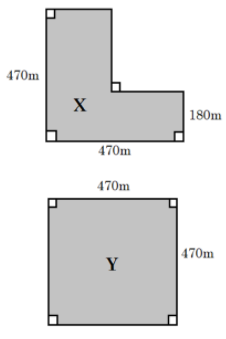
Here in this problem, we are given a diagram showing two fields X and Y with their dimensions. The cost of fencing these fields is $Rs.40$ per meter. The cost of field X and Y is given as ${C_X}$ and ${C_Y}$ . Now using this information we need to figure out which of the four given options is correct.
You must understand that the fencing will always be done exactly on the boundary of the field. Therefore, to find the total length of fencing required for both fields we must find out the perimeter of the fields. The perimeter of any two-dimensional polygon can be found by adding up the lengths of each side.

For field X, the total length of fencing $ = $ Sum of the lengths of all sides $ = $ Perimeter of X
$ \Rightarrow $ Perimeter of X $ = 470 + (180 + 290) + \left( {290 + 180} \right) + 470$
Now, these dimensions of sides of the field can be easily added as:
$ \Rightarrow $ Perimeter of X $ = 470 + 470 + 470 + 470 = 4 \times 470 = 1880{\text{m}}$
Similarly, for field Y, the total length of fencing $ = $ Sum of the lengths of all sides $ = $ Perimeter of Y
$ \Rightarrow $ Perimeter of Y $ = 470 + 470 + 470 + 470 = 4 \times 470 = 1880{\text{m}}$
For calculating the total cost of fencing be must multiply the perimeter with the rate off fencing, i.e. $Rs.40$ per meter
$ \Rightarrow $Cost of fencing X, i.e. ${C_X} = 1880 \times 40 = Rs.75200$
Similarly,
$ \Rightarrow $Cost of fencing Y, i.e. ${C_Y} = 1880 \times 40 = Rs.75200$
Therefore, we get ${C_X} = {C_Y}$
Hence, the option (A) is the correct answer.
Note:
In mensuration, the use of the fundamental concept of area and perimeter. An alternative approach to check for the relationship between ${C_X}$ and ${C_Y}$ can be taken by comparing the areas of the field X and Y. Since the rate of fencing is the same for both fields, the relation between the perimeter will be the same as the cost of fencing, i.e. ${C_X}$ and ${C_Y}$.
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
Who is known as the "Little Master" in Indian cricket history?

Explain the Treaty of Vienna of 1815 class 10 social science CBSE

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Which are the three major ports of Tamil Nadu A Chennai class 10 social science CBSE

The highest dam in India is A Bhakra dam B Tehri dam class 10 social science CBSE

Describe the process of Unification of Italy class 10 social science CBSE




