
Express each number as a product of its prime numbers:
(i) 140
(ii) 156
(iii) 3825
(iv) 5005
(v) 7429
Answer
512.7k+ views
Hint: First understand that the given numbers have to be divided by prime numbers which are also the factors of the numbers. Then convert the numbers into the product of its prime factors and write it as it is.
“Complete step-by-step answer:”
We are given some numbers and asked to express them as a product of their prime factors.
First we will understand what a prime factor is.
A prime factor is a prime number. In other words any of the prime numbers that will be multiplied to give the original number is a prime factor.
For example: $15=3\times 5$, here 3 and 5 are prime numbers and factors of 15.
We will find the prime factors by dividing the number by the prime number until its quotient is a prime number or 1.
In this question the numbers given are,
(i) 140 (ii) 156 (iii) 3825 (iv) 5005 (v) 7429
Let’s take 140,

Now 140 can be expressed as $2\times 2\times 5\times 7$.
So, $140={{2}^{2}}\times 5\times 7$
Let’s take 156,

Now 156 can be expressed as $2\times 2\times 3\times 13$.
So, $156={{2}^{2}}\times 3\times 13$.
Let’s take 3825.
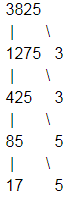
Now 3825 can be expressed as $3\times 3\times 5\times 5\times 17.$
So, $3825={{3}^{2}}\times {{5}^{2}}\times 17.$
Let’s take 5005,

Now 5005 can be expressed as $5\times 7\times 11\times 13.$
So, $5005=5\times 7\times 11\times 13.$
Let’s take 7429,
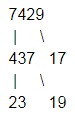
Now 7429 can be expressed as $17\times 19\times 23.$
So, $7429=17\times 19\times 23.$
So the required answer is
$\begin{align}
& 140={{2}^{2}}\times 5\times 7 \\
& 156={{2}^{2}}\times 3\times 13 \\
& 3825={{3}^{2}}\times {{5}^{2}}\times 17 \\
& 5005=5\times 7\times 11\times 13 \\
& 7429=17\times 19\times 23 \\
\end{align}$
Note: While dividing the students must be careful about calculations because any mistake will make your whole answer wrong. Students should choose their divisors which are prime numbers and should use their prime factors for division according to ascending order to avoid any kind of errors or mistakes in their answers.
“Complete step-by-step answer:”
We are given some numbers and asked to express them as a product of their prime factors.
First we will understand what a prime factor is.
A prime factor is a prime number. In other words any of the prime numbers that will be multiplied to give the original number is a prime factor.
For example: $15=3\times 5$, here 3 and 5 are prime numbers and factors of 15.
We will find the prime factors by dividing the number by the prime number until its quotient is a prime number or 1.
In this question the numbers given are,
(i) 140 (ii) 156 (iii) 3825 (iv) 5005 (v) 7429
Let’s take 140,

Now 140 can be expressed as $2\times 2\times 5\times 7$.
So, $140={{2}^{2}}\times 5\times 7$
Let’s take 156,

Now 156 can be expressed as $2\times 2\times 3\times 13$.
So, $156={{2}^{2}}\times 3\times 13$.
Let’s take 3825.
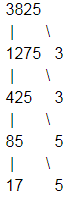
Now 3825 can be expressed as $3\times 3\times 5\times 5\times 17.$
So, $3825={{3}^{2}}\times {{5}^{2}}\times 17.$
Let’s take 5005,

Now 5005 can be expressed as $5\times 7\times 11\times 13.$
So, $5005=5\times 7\times 11\times 13.$
Let’s take 7429,
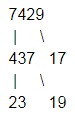
Now 7429 can be expressed as $17\times 19\times 23.$
So, $7429=17\times 19\times 23.$
So the required answer is
$\begin{align}
& 140={{2}^{2}}\times 5\times 7 \\
& 156={{2}^{2}}\times 3\times 13 \\
& 3825={{3}^{2}}\times {{5}^{2}}\times 17 \\
& 5005=5\times 7\times 11\times 13 \\
& 7429=17\times 19\times 23 \\
\end{align}$
Note: While dividing the students must be careful about calculations because any mistake will make your whole answer wrong. Students should choose their divisors which are prime numbers and should use their prime factors for division according to ascending order to avoid any kind of errors or mistakes in their answers.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 English: Engaging Questions & Answers for Success

Why are manures considered better than fertilizers class 11 biology CBSE

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Which one of the following groups comprises states class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

A couple went for a picnic They have 5 sons and each class 8 maths CBSE

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE




