Question

Explain why square is also a parallelogram ?

Answer 1

Hint: A square has all the properties of a parallelogram and also has some additional properties. So, let us draw a square ABCD and state all its properties.

Complete step-by-step answer:

As we know that the properties of a parallelogram can be stated according to the sides, the angles, the diagonals and the symmetry.
So, the properties of parallelogram are,
It has 2 pairs of opposite sides parallel.
It has 2 pairs of opposite sides equal.
The sum of the angles of a parallelogram is equal to \[360^\circ \],
2 pairs of opposite angles of a parallelogram are equal.
The diagonals of a parallelogram bisect each other.
A parallelogram has 2 lines of symmetry.
Now as we know that all of the above stated properties also apply to squares. So, it can be considered to be a parallelogram. However, a square has additional properties as well, so it can be regarded as a special type of parallelogram.
A square has :
2 pairs of opposite sides parallel
All its sides equal.
The sum of the angles of a square is equal to \[360^\circ \].
All the angles of a square are equal to \[90^\circ \].
The diagonals of a square bisect each other at \[90^\circ \], diagonals of a square are equal, and the diagonals bisect the angles at the vertices to give \[45^\circ \].
A square has 4 lines of symmetry.
So, now we can see from the above properties of the square that all the properties of a parallelogram also apply to the square.

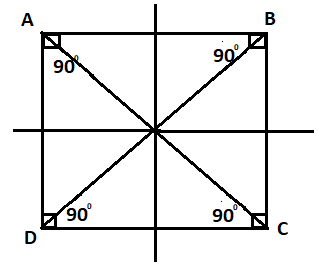
So, that’s why parallelograms are also square.

Note: Whenever we come up with this type of problem then we should remember that the squares, rectangles and rhombus are the special type of parallelogram because all the properties of a parallelogram also apply to the square, rectangle and rhombus however they have some additional properties which parallelogram does not have. So, all parallelograms are not square, rectangles and rhombus.