Question

Explain why a rectangle is a convex quadrilateral.

Answer 1

Hint: To solve this question we need to know about a convex quadrilateral. A convex quadrilateral is a four-sided polygon which has each interior angle measures less than $180{}^\circ $ and all the diagonals lie within the quadrilateral. We will use this definition to give the answer.

Complete step by step answer:
Now, we know that rectangle is a quadrilateral in which opposite sides are equal and parallel. A rectangle has four right angles. Diagonals of a rectangle bisect each other.
Now, we know that a convex quadrilateral is a four-sided polygon which has each interior angle measures less than $180{}^\circ $ and all the diagonals lie within the quadrilateral.

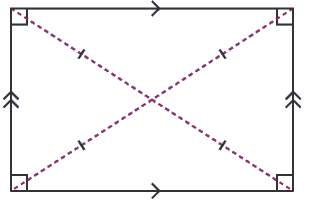
So, from the above discussion, we can conclude that a rectangle has each interior angle measures less than $180{}^\circ $ and has all the diagonals lie within the shape. So we can say that a rectangle is a convex quadrilateral.
So, the given statement is true. Option A is the correct answer.
Note:
 To solve such type of question students must draw a diagram of polygon and draw the diagonals by joining the opposite corners. Then observe the figure that it will fulfill the criterion to be convex or not. We need to check each interior angle of the polygon. Then give the answer.