Question

 Explain the phenomenon of total internal reflection of light with an example. Draw necessary ray of diagram.

Answer 1

Hint: Total internal reflection is the phenomenon of bouncing back of light in the same medium after striking the boundary of a rarer medium. This happens when the angle of refraction exceeds ${{90}^{\circ }}$. In such a case Snell’s law becomes invalid and reflection takes place instead of refraction.

Complete step by step answer:
 Refraction is the process of bending of light rays when they travel from one medium to another medium. If a light ray travels from medium of refractive index \[{{\mu }_{1}}\], making an angle $\theta $ (angle between the normal at boundary of mediums and incident ray) to a medium of refractive index \[{{\mu }_{2}}\], making an angle $r$ (angle between the normal of boundary of mediums and refracted ray), then by Snell’s law we can say that
${{\mu }_{1}}\sin \theta ={{\mu }_{2}}\sin r$
For any two mediums, the medium with lesser refractive index is called rarer medium while the medium with higher refractive index is called denser medium. When light rays travel from rarer medium to denser medium, light rays bends towards the normal. When light rays travel from denser medium to rarer medium, light rays bends away from the normal. Total internal reflection is a phenomenon which takes place when light travels from denser medium to rarer medium. Critical angle is angle of incidence for which angle of refraction is a right angle. When the angle of incidence is increased, angle of refraction also increases, but when angle of incidence exceeds critical angle, light ray is totally reflected back to the same medium i.e. no refraction of light. This phenomenon is called total internal reflection.

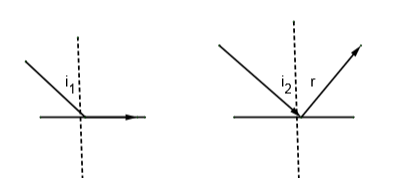
 Applying Snell’s law at critical angle, we get
$\begin{align}
  & {{\mu }_{d}}\sin {{i}_{c}}={{\mu }_{r}}\sin {{90}^{\circ }} \\
 & \sin {{i}_{c}}=\dfrac{{{\mu }_{r}}}{{{\mu }_{d}}} \\
\end{align}$
where ${{\mu }_{d}}$ is refractive index of denser medium ${{\mu }_{r}}$ is refractive index of rarer medium and ${{i}_{c}}$ is critical angle.
For total internal reflection, angle of incidence must be greater than critical angle.
Note: The phenomenon of refraction takes place only when light rays travel from denser to rarer medium. This is because when light rays travel from rarer to denser medium, refracted angle is always smaller than incident angle (angle of incidence can never exceed ${{90}^{\circ }}$ as a result angle of refraction can also never exceed ${{90}^{\circ }}$, so total internal refraction cannot take place).