Question

Explain positive, negative and zero work. Give one example of each.

Answer 1

Hint: Write formula of work $W=\overrightarrow{F}\cdot \overrightarrow{r}$. Learn dot product of two forces. For positive work, W should be positive so for this find an angle between force and displacement.
Dot product of two component A and B
$\overrightarrow{A}\cdot \overrightarrow{B}=AB\cos \theta $
Where $\theta $ is the angle between two vectors.
$\overrightarrow{F}\cdot \overrightarrow{r}=Fr\cos \theta $
Find $\theta $ for positive W, negative W and zero W.

Complete step by step answer:
The work done by a force on a particle during a displacement is given as
$W=\overrightarrow{F}\cdot \overrightarrow{r}$
Here, W = work
$\overrightarrow{F}$= force
$\overrightarrow{r}$= displacement
Positive work done – The work done is said to be positive when force and displacement are in the same direction.
$\begin{align}
  & \theta ={{0}^{{}^\circ }} \\
 & \overrightarrow{F}\cdot \overrightarrow{r}=Fr\cos \theta \\
 & \overrightarrow{F}\cdot \overrightarrow{r}=Fr\cos {{0}^{{}^\circ }} \\
 & \overrightarrow{F}\cdot \overrightarrow{r}=Fr \\
 & W=\overrightarrow{F}\cdot \overrightarrow{r}=Fr \\
\end{align}$

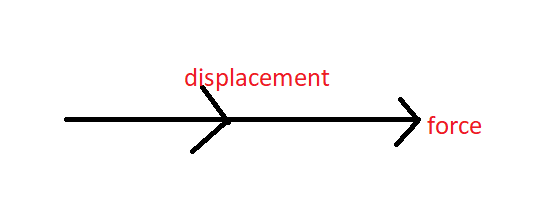
Hence, work is positive.

Zero work – the work done is said to be zero when force and displacement are perpendicular to each other.
$\begin{align}
  & \theta ={{90}^{{}^\circ }} \\
 & \overrightarrow{F}\cdot \overrightarrow{r}=Fr\cos \theta \\
 & \overrightarrow{F}\cdot \overrightarrow{r}=Fr\cos {{90}^{{}^\circ }} \\
 & \overrightarrow{F}\cdot \overrightarrow{r}=0 \\
 & W=\overrightarrow{F}\cdot \overrightarrow{r}=0 \\
\end{align}$
Hence, work is zero

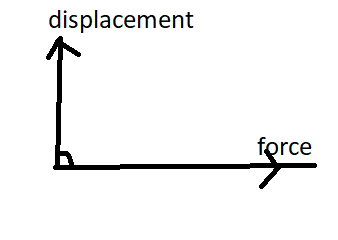
Negative work done – The work done is said to be negative when force and displacement are in opposite directions.

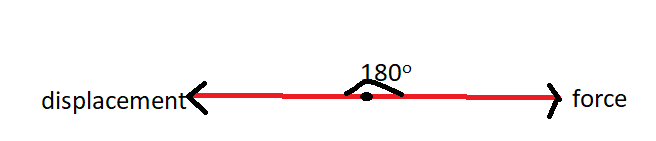
$\begin{align}
  & \theta ={{180}^{{}^\circ }} \\
 & \overrightarrow{F}\cdot \overrightarrow{r}=Fr\cos \theta \\
 & \overrightarrow{F}\cdot \overrightarrow{r}=Fr\cos {{180}^{{}^\circ }} \\
 & \overrightarrow{F}\cdot \overrightarrow{r}=-Fr \\
 & W=\overrightarrow{F}\cdot \overrightarrow{r}=-Fr \\
\end{align}$
Hence, work is negative.

Note: Work done by friction is always zero because friction force and displacement act in opposite directions. When a spring travels from A to B and from B back to A then work done during the return journey is negative of the work during the onwards journey and the net work done by the spring is zero.