Question

Explain how friction helps us to walk?

Answer 1

Hint: As you all know, the frictional force arises from the contact between two surfaces. So, a normal reaction by the foot on to the ground gives rise to frictional force, which pushes us forward.

Complete step by step solution:
First Example:

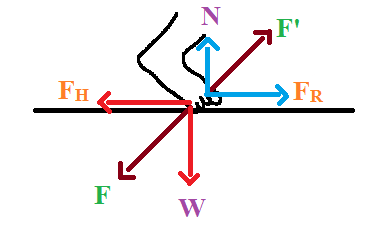
When you try to walk, you will apply a downward force \[\text{F}\] onto the ground, a resultant force \[\text{F }\!\!'\!\!\text{ }\] will be produced which is equal and opposite to the applied force \[\text{F}\] according to Newton's third law of motion. So we can write, \[\text{F}=-\text{F}'\].
If we resolve the force \[\text{F}\], that we apply to the ground to different components, we will get a component called the weight $\text{(W)}$ acting on the foot acting downwards and the effective horizontal force $\text{(}{{\text{F}}_{\text{H}}}\text{)}$ acting on the foot which is directed to the left side of the foot.
If we try to resolve the resultant force \[\text{F }\!\!'\!\!\text{ }\] into components, we will get a component called the normal component which is acting upwards $\text{(N)}$ (opposite to the weight) and horizontal component of friction $\text{(}{{\text{F}}_{\text{R}}}\text{)}$ which is directed to the right side of the foot (opposite to the effective horizontal force).
The horizontal frictional force acting towards the right, which acts opposite to the effective horizontal force applied by our foot prevents us from slipping while walking.
Second Example:

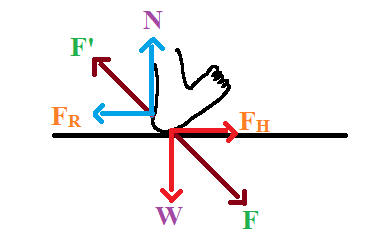
When you try to walk, you will apply a downward force \[\text{F}\] onto the ground, a resultant force \[\text{F }\!\!'\!\!\text{ }\] will be produced which is equal and opposite to the applied force \[\text{F}\] according to Newton's third law of motion. So we can write, \[\text{F}=-\text{F}'\].
If we resolve the force \[\text{F}\], that we apply to the ground to different components, we will get a component called the weight $\text{(W)}$ acting on the foot acting downwards and the effective horizontal force $\left( {{\text{F}}_{\text{H}}} \right)$ acting on the foot which is directed to the right side of the foot in this case.
If we try to resolve the resultant force \[\text{F }\!\!'\!\!\text{ }\] into components, we will get a component called the normal component $\text{(N)}$ which is acting upwards (opposite to the weight) and horizontal component of friction $\text{(}{{\text{F}}_{\text{R}}}\text{)}$ which is directed to the left side of the foot in this case(opposite to the effective horizontal force).
The horizontal frictional force acting towards the left, which acts opposite to the effective horizontal force applied by our foot prevents us from slipping while walking.

Note: Even if friction is considered as a dissipative force, it helps in many circumstances, one which is mentioned in the answer. We can refer to frictional force as a necessary evil.
There are two types of friction,
Static Friction: It is the friction associated with a body at rest. So if we want to move a body by applying a force on it, we need to overcome the force of friction first in order to do it.
Kinetic Friction: It is the friction associated with the bodies in motion. It acts against the motion of a body in a particular direction.