Question

How do you expand ${\left( {x - 5} \right)^6}$ using Pascal’s triangle?

Answer 1

Hint: We first write the binomial expansion of ${\left( {x - 5} \right)^6}$. Then we explain Pascal's triangle and the use it. We explain how the coefficients work. We also explain the use of the constant a and n in the general expansion of ${\left( {x + a} \right)^n}$. Then we find the coefficients of the equation ${\left( {x - 5} \right)^6}$ using Pascal’s triangle.

Complete step-by-step answer:
First, we write down the binomial expansion of the given equation ${\left( {x - 5} \right)^6}$, then we explain it with the help of Pascal’s triangle.
$ \Rightarrow {\left( {x - 5} \right)^6} = {x^6} - 30{x^5} + 375{x^4} - 2500{x^3} + 9375{x^2} - 18750x + 15625$
Pascal’s triangle helps to find the coefficients for the expansion of the ${\left( {x - 5} \right)^6}$, where n decides the number of times, we continue with the triangle expansion and the added value with x (for general case a) decides the multiplier. We multiply with ${a^n}$, $a = 0\left( 1 \right)n$ consecutively.
We first draw the triangle values till the ${7^{th}}$ row where it starts with 1 at the top.

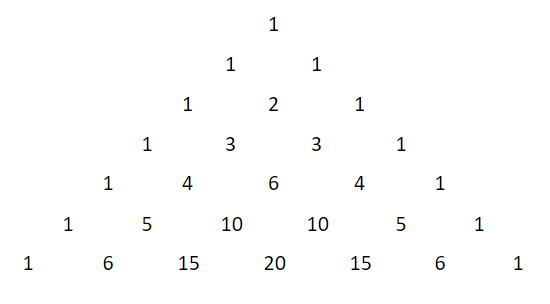
Every coefficient is the addition of the previous two coefficients on its top. These coefficients are made for the expansion of the term ${\left( {x + 1} \right)^n}$. For particular we took the value of $n = 6$ and that’s why we took 6 rows after the first value of 1 at the top.
Now instead of a, we have to multiply with -5 as for the equation ${\left( {x - 5} \right)^6}$ we have $a = - 5$.
The relative coefficients are 1, 6, 15, 20, 15, 6 ,1. We multiply them with${\left( { - 5} \right)^0},{\left( { - 5} \right)^1},{\left( { - 5} \right)^2},{\left( { - 5} \right)^3},{\left( { - 5} \right)^4},{\left( { - 5} \right)^5},{\left( { - 5} \right)^6}$ respectively.
Therefore, the actual coefficients are,
$ \Rightarrow {\left( { - 5} \right)^0} \times 1,{\left( { - 5} \right)^1} \times 6,{\left( { - 5} \right)^2} \times 15,{\left( { - 5} \right)^3} \times 20,{\left( { - 5} \right)^4} \times 15,{\left( { - 5} \right)^5} \times 6,{\left( { - 5} \right)^6} \times 1$
Simplify the terms,
$ \Rightarrow 1, - 30,375, - 2500,9375, - 18750,15625$

Hence, the expansion of ${\left( {x - 5} \right)^6}$ is ${x^6} - 30{x^5} + 375{x^4} - 2500{x^3} + 9375{x^2} - 18750x + 15625$.

Note:
In binomial expansion, these coefficients are used in the form of combination where the expansion is
${\left( {x + a} \right)^n} = {}^n{C_0}{x^n}{a^0} + {}^n{C_1}{x^{n - 1}}{a^1} + \ldots + {}^n{C_r}{x^{n - r}}{a^r} + \ldots + {}^n{C_{n - 1}}{x^1}{a^{n - 1}} + {}^n{C_n}{x^0}{a^n}$
The general coefficient value for ${\left( {r + 1} \right)^{th}}$ term is ${}^n{C_r}$ where ${}^n{C_n} = \dfrac{{n!}}{{r!\left( {n - r} \right)!}}$.