Question

Examine the table.
(Each figure is divided into triangles and the sum of the angles deduced from that.)
What can you say about the angle sum of a convex polygon with the number of sides?
a) 7
b) 8
c) 10
d) $n$

Figure
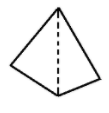
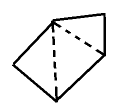
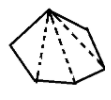
Side	3	4	5	6
Angle sum	${180^ \circ }$	$ 2 \times {180^ \circ } \\ = \left( {4 - 2} \right) \times {180^ \circ } \\ $	$ 3 \times {180^ \circ } \\ = \left( {5 - 2} \right) \times {180^ \circ } \\ $	$ 4 \times {180^ \circ } \\ = \left( {6 - 2} \right) \times {180^ \circ } \\ $

Answer 1

Hint: We are given the angle sum of polygons with the number of sides as 3, 4, 5 and 6. We will follow the pattern as given in the question. We will replace the number of sides in the pattern with 7, 8, 10 and \[n\] to get the required answer.

Complete step by step solution: We are given that a polygon with 3 sides has angle sum equals to ${180^ \circ }$, a polygon with 4 sides has angle sum equals to $2 \times {180^ \circ } = \left( {4 - 2} \right) \times {180^ \circ }$, a polygon with 5 sides has angle sum equals to $3 \times {180^ \circ } = \left( {5 - 2} \right) \times {180^ \circ }$ and a polygon with 6 sides has angle sum equals to $4 \times {180^ \circ } = \left( {6 - 2} \right) \times {180^ \circ }$
We have to find the angle sum when the number of sides is 7.
Following the given pattern, we have the angle sum as $\left( {7 - 2} \right) \times {180^ \circ } = 5 \times {180^ \circ }$
Hence, the angle sum of the polygon with 3 sides is equal to ${900^ \circ }$
Similarly, we can write the angle sum of polygon with 8 sides as $\left( {8 - 2} \right) \times {180^ \circ } = 6 \times {180^ \circ }$
On solving it, we get the angle sum equals to ${1080^ \circ }$
Now, the sum of angles with 10 sides is $\left( {10 - 2} \right) \times {180^ \circ } = 8 \times {180^ \circ }$
Therefore, the angle sum of polygons with 8 sides is ${1440^ \circ }$
Now, generalising the formula, with $n$ sides, the angle sum is equal to $\left( {n - 2} \right) \times {180^ \circ }$

Note: Angle sum refers to the sum of all the interior angles of the polygon. It is fixed for the polygons with the same number of sides. A polygon with three sides is known as the triangle, a polygon with 4 sides is known as a quadrilateral, with 5 sides, it is known as a pentagon and so on.