
How do you evaluate \[\sin \left( \dfrac{\pi }{3} \right)\]?
Answer
555k+ views
Hint: To calculate the value of \[\sin \left( \dfrac{\pi }{3} \right)\], firstly we have to change the angle in a form that is easily understood by us. The given question has the angle given in radians, so we will convert it into degrees keeping in mind the conversion factor for radian and degrees, which is \[\pi \] radians \[={{180}^{\circ }}\] and then apply the trigonometric function to the angle to get the final value of the expression.
Complete step by step answer:
The trigonometric functions can have the angle in two forms namely: degrees and radians. We have studied mostly in degrees and it is more convenient. But both these forms are interconvertible. Since radian form is hard to interpret so we generally convert the angle given in radian to degrees so that it becomes much more understandable.
The conversion factor for degrees can be stated as:
\[\pi \] radians \[={{180}^{\circ }}\]
Or \[1rad.=\dfrac{{{180}^{\circ }}}{\pi }\]
We are given the question to solve for \[\sin \left( \dfrac{\pi }{3} \right)\],
Sine function has values ranging from 0 to 1 in the first quadrant(\[{{0}^{\circ }}-{{90}^{\circ }}\]).
To solve \[\sin \left( \dfrac{\pi }{3} \right)\], we first need to solve which angle in degrees is \[\dfrac{\pi }{3}\].
\[\dfrac{\pi }{3}\] is an angle given in radians. Since we now know the relation between degrees and radian, we simply need to convert into the appropriate form (that is into degrees).
Converting \[\dfrac{\pi }{3}\], we have,
\[\dfrac{\pi }{3}=\dfrac{\pi }{3}\times \dfrac{{{180}^{\circ }}}{\pi }\] (as we know \[1rad.=\dfrac{{{180}^{\circ }}}{\pi }\])
\[\pi \] is present both in numerator and denominator and so gets cancelled we now get,
\[\Rightarrow \dfrac{{{180}^{\circ }}}{3}={{60}^{\circ }}\]
So we can conclude that, \[\dfrac{\pi }{3}={{60}^{\circ }}\]
Putting this value in sine function we have,
\[\sin \left( {{60}^{\circ }} \right)\]
We now have to recall the special triangle with the help of which we can find the value of \[\sin \left( {{60}^{\circ }} \right)\].
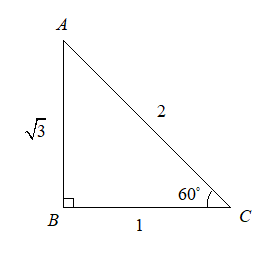
As we know, \[\sin \theta =\dfrac{perpendicular}{hypotenuse}\]
From the triangle, we can figure out the value of \[\sin \left( {{60}^{\circ }} \right)\]
Therefore, we have \[\sin ({{60}^{\circ }})=\dfrac{\sqrt{3}}{2}\]
Note: While converting the angle from radians to degree, \[\pi \] radians can be directly taken or substituted for \[{{180}^{\circ }}\]but for converting into radians do not skip any step as it can lead to wrong answer.
\[1\deg .=\dfrac{\pi }{{{180}^{\circ }}}\] (this formula can be applied)
Complete step by step answer:
The trigonometric functions can have the angle in two forms namely: degrees and radians. We have studied mostly in degrees and it is more convenient. But both these forms are interconvertible. Since radian form is hard to interpret so we generally convert the angle given in radian to degrees so that it becomes much more understandable.
The conversion factor for degrees can be stated as:
\[\pi \] radians \[={{180}^{\circ }}\]
Or \[1rad.=\dfrac{{{180}^{\circ }}}{\pi }\]
We are given the question to solve for \[\sin \left( \dfrac{\pi }{3} \right)\],
Sine function has values ranging from 0 to 1 in the first quadrant(\[{{0}^{\circ }}-{{90}^{\circ }}\]).
To solve \[\sin \left( \dfrac{\pi }{3} \right)\], we first need to solve which angle in degrees is \[\dfrac{\pi }{3}\].
\[\dfrac{\pi }{3}\] is an angle given in radians. Since we now know the relation between degrees and radian, we simply need to convert into the appropriate form (that is into degrees).
Converting \[\dfrac{\pi }{3}\], we have,
\[\dfrac{\pi }{3}=\dfrac{\pi }{3}\times \dfrac{{{180}^{\circ }}}{\pi }\] (as we know \[1rad.=\dfrac{{{180}^{\circ }}}{\pi }\])
\[\pi \] is present both in numerator and denominator and so gets cancelled we now get,
\[\Rightarrow \dfrac{{{180}^{\circ }}}{3}={{60}^{\circ }}\]
So we can conclude that, \[\dfrac{\pi }{3}={{60}^{\circ }}\]
Putting this value in sine function we have,
\[\sin \left( {{60}^{\circ }} \right)\]
We now have to recall the special triangle with the help of which we can find the value of \[\sin \left( {{60}^{\circ }} \right)\].
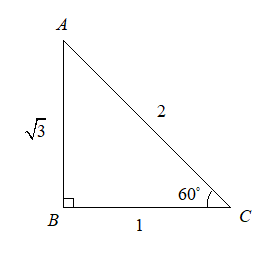
As we know, \[\sin \theta =\dfrac{perpendicular}{hypotenuse}\]
From the triangle, we can figure out the value of \[\sin \left( {{60}^{\circ }} \right)\]
Therefore, we have \[\sin ({{60}^{\circ }})=\dfrac{\sqrt{3}}{2}\]
Note: While converting the angle from radians to degree, \[\pi \] radians can be directly taken or substituted for \[{{180}^{\circ }}\]but for converting into radians do not skip any step as it can lead to wrong answer.
\[1\deg .=\dfrac{\pi }{{{180}^{\circ }}}\] (this formula can be applied)
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




