Question

How do you evaluate $\sin \left( {\arctan \left( 3 \right)} \right)$?

Answer 1

Hint: We explain the function $arc\tan \left( x \right)$. We express the inverse function of tan in the form of $arc\tan \left( x \right) = {\tan ^{ - 1}}x$. We draw the graph of $arc\tan \left( x \right)$ and the line $x = 3$ to find the intersection point. Thereafter we take the sin ratio of that angle to find the solution.

Complete step by step answer:
The given expression is the inverse function of the trigonometric ratio tan.
The arcus function represents the angle which on ratio tan gives the value.
So, $arc\tan \left( x \right) = {\tan ^{ - 1}}x$. If $arc\tan \left( x \right) = \alpha $ then we can say $\tan \alpha = x$.
Each of the trigonometric functions is periodic in the real part of its argument, running through all its values twice in each interval of $2\pi $.
The general solution for that value where $\tan \alpha = x$ will be $n\pi + \alpha ,n \in \mathbb{Z}$.
But for $arc\tan \left( x \right)$, we won’t find the general solution. We use the principal value. For ratio tan we have $ - \dfrac{\pi }{2} \leqslant arc\tan \left( x \right) \leqslant \dfrac{\pi }{2}$.
The graph of the function is

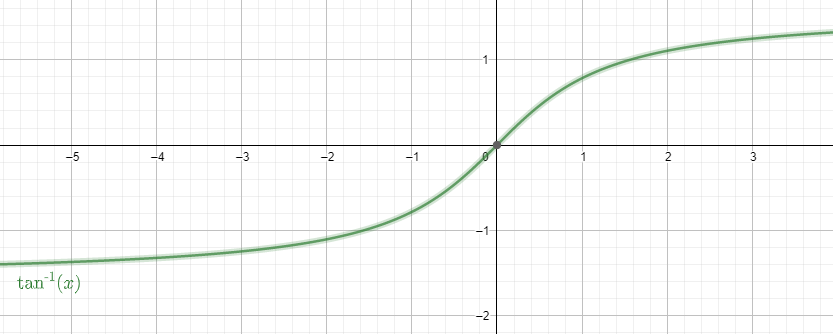
We now place the value of $x = 3$ in the function of $arc\tan \left( x \right)$.
Let the angle be $\theta $ for which $arc\tan \left( 3 \right) = \theta $. This gives $\tan \theta = 3$.
For this we take the line of $x = 3$ and see the intersection of the line with the graph $arc\tan \left( x \right)$.

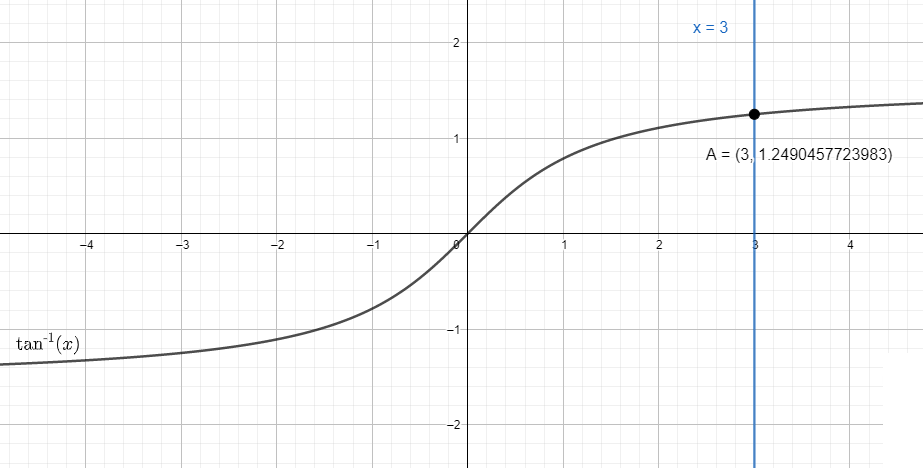
Putting the value in the graph of $arc\tan \left( x \right)$, we get $\theta = 71.56$. (approx.)
We get the value of y coordinates as $71.56$.
Now we take $\sin \left( {\arctan \left( 3 \right)} \right) = \sin \left( {71.56} \right) = 0.948$.
Therefore, the value of $\sin \left( {\arctan \left( 3 \right)} \right)$ is $0.948$.

Note:
 We can also apply the trigonometric identity where $\tan \theta = 3$. We express it in a right-angle triangle whose height will be 3 and the base will be 1.
In that case the hypotenuse will be $\sqrt {{3^2} + {1^2}} = \sqrt {10} $.

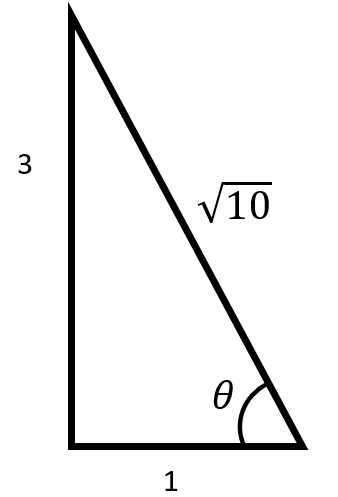
Also, in the exact solution domain of $ - \dfrac{\pi }{2} \leqslant \theta \leqslant \dfrac{\pi }{2}$, using those identities we get $\sin \theta = \dfrac{{{\text{height}}}}{{hypotenuse}} = \dfrac{3}{{\sqrt {10} }}$.
As $arc\tan \left( 3 \right) = \theta $, the value of $\sin \left( {\arctan \left( 3 \right)} \right) = \sin \theta = \dfrac{3}{{\sqrt {10} }}$. The value of $\dfrac{3}{{\sqrt {10} }} = 0.948$.