Question

Equation of the tangent at the vertex of the parabola \[{x^2} + 4x + 4y + 16 = 0\] is
A. \[y + 3 = 0\]
B. \[y + 4 = 0\]
C. \[y + 2 = 0\]
D. \[y + 1 = 0\]

Answer 1

Hint:Here in the given question we have to find the equation of the tangent at the vertex of the given parabolic equation. To know this equation we need to equate the given parabolic equation with the standard equation of parabola and find the vertex. A tangent is a line which is in contact with parabola by satisfying necessary conditions.

Complete step by step answer:
 From the question given we have the equation of parabola is
\[ \Rightarrow \]\[{x^2} + 4x + 4y + 16 = 0\] -------- (1)
On rearranging the equation (1) we get
\[ \Rightarrow \]\[{x^2} + 4x + 16 + 4y = 0\] -------- (2)
On adding and subtracting 4 to the equation (2) we get
\[ \Rightarrow \]\[{x^2} + 4x + 4 + 4y + 16 - 4 = 0\] -------- (3)
On simplifying equation (3)
\[ \Rightarrow \]\[{x^2} + 2 \times 2 \times x + {2^2} + 4y + 12 = 0\] -------- (4)
On rearranging equation (4) we get
\[ \Rightarrow \]\[{\left( {x + 2} \right)^2} + 4y + 12 = 0\] --------- (5)
\[ \Rightarrow \]\[{\left( {x + 2} \right)^2} = - 4\left( {y + 3} \right)\] --------- (6)
On comparing equation (6) with the standard equation of vertical parabola that is \[{x^2} = - 4Ay\], here the value of A =1 which is positive quantity. We have to note the equation has a negative sign, which indicates that the parabola is formed in the negative y-axis as shown in the diagram. On the axis of parabola vertex will be -1 unit from the focus and hence the equation of tangent at vertex is \[y = - 3\].
\[ \therefore y + 3 = 0\]

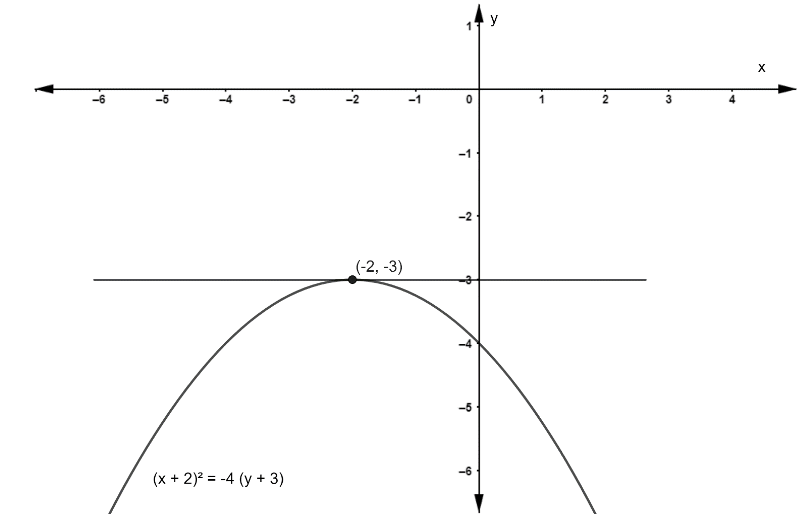
Therefore, the correct option is A.

Note: Here we need to remember that always the equation of parabola must be in the standard form in the given equation we need to modify and simplify the equation to the standard form of parabola. As tangents is an equation of line touching a parabola at a point can be represented as \[y = mx + c\].