Question

Energy stored in between plates of parallel plate capacitor of area A, separated by distance d is:
\[\begin{align}
  & A.~~~~~~~\dfrac{{{\varepsilon }_{0}}{{E}^{2}}Ad}{2}~~~~ \\
 & B.~~~~~~~\dfrac{{{\varepsilon }_{0}}{{E}^{2}}A}{2d}~~~~~ \\
 & C.~~~~~~~\dfrac{{{\varepsilon }_{0}}d}{2{{E}^{2}}A}~~~~ \\
 & D.~~~~~~\dfrac{Ad}{2{{\varepsilon }_{0}}{{E}^{2}}}~~~~ \\
\end{align}\]

Answer 1

Hint: Energy stored in a system is the total amount of work done to form the system. So, in order to calculate energy stored in between plates of parallel plate capacitors, we will calculate total work done to form it. For this we will calculate the word required to shift charge from one plate of capacitor to another.

Formula Used:
The work done to move charge q through a potential difference V is
$W=qV$
Capacitance of a parallel plate capacitor having potential difference V between its plates is given by
$c=\dfrac{q}{V}$
Capacitance of a parallel plate capacitor of area A, distance between plates d is
$c=\dfrac{{{\varepsilon }_{0}}A}{d}$
Electric field between capacitor plates E is
$E=\dfrac{V}{d}$

Complete Step By Step Solution:
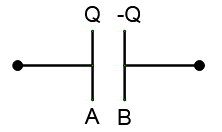
Initially let us consider two capacitor plates A & B each with zero charge. Now, slowly charge is shifted from B to A till charge on A becomes Q and till charge on B becomes –Q

Suppose at time t, charge shifted is equal to q. So charge on A is q and charge on B is –q. Now if we further shift $dq$ (where,$dq\to 0$ ) from B to A,

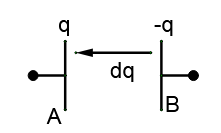
The work done for this will be given by
$dW=dq\times V$ … (1)
where $dq$ is a small charge and V is a potential difference between plates.
For capacitor we can say-
$c=\dfrac{q}{V}$
$V=\dfrac{q}{c}$
Putting this value of V in equation 1-
$dW=\dfrac{q}{c}dq$
Capacitance of all capacitors depends only on the dimension of plates and distance between them. So capacitance will be constant for a given capacitor.
To calculate total work done in forming capacitor we will integrate this with limit of q from 0 to Q,
$\int{dW}=\int\limits_{0}^{Q}{\dfrac{q}{c}dq}$
On solving this we get
$W=\dfrac{{{Q}^{2}}}{2c}$
For capacitor we can say
$c=\dfrac{q}{V}$
$Q=cV$
Putting this value of Q in $W=\dfrac{{{Q}^{2}}}{2c}$we get
$W=\dfrac{c{{V}^{2}}}{2}$
Also electric field between capacitor plates E is
$E=\dfrac{V}{d}$
$V=Ed$
Putting this value of V in $W=\dfrac{c{{V}^{2}}}{2}$ we get
$W=\dfrac{c{{E}^{2}}{{d}^{2}}}{2}$
Also for capacitor we can say
$c=\dfrac{{{\varepsilon }_{0}}A}{d}$
Putting this value of c in $W=\dfrac{c{{E}^{2}}{{d}^{2}}}{2}$
\[W=\dfrac{1}{2}\times \dfrac{{{\varepsilon }_{0}}A}{d}\times {{E}^{2}}{{d}^{2}}=\dfrac{{{\varepsilon }_{0}}{{E}^{2}}Ad}{2}~~~\]
So the correct option is A.

Note: V in all the formulae is the potential difference between the plates, not the actual potential of any of them. The electric field anywhere between the capacitor plates is constant and has its magnitude equals to
$E=\dfrac{V}{d}$ .
This question can also be done by using the formula of electric field density, which is
$E=\dfrac{{{\varepsilon }_{0}}{{E}^{2}}}{2}$
If this will be multiplied by total volume (product of area of plates and distance between them) between capacitor we will get our answer
$\dfrac{{{\varepsilon }_{0}}{{E}^{2}}}{2}\times Ad=\dfrac{{{\varepsilon }_{0}}{{E}^{2}}Ad}{2}~~$