Question

What is electrical resistivity of a material? What is its unit? Describe an experiment to study the factors on which the resistance of conducting wire depends.

Answer 1

Hint: Electrical resistivity (also known as particular electrical resistance or volume resistivity) is a material attribute that determines how well it resists electric current.Electrical conductivity, its inverse, measures how well a material conducts electricity.

Complete step by step answer:
Resistivity:Resistivity is defined as the resistance of a conductor with a length of \[1m\] and a cross sectional area of \[1{m^2}\] .
$R = \dfrac{{\rho \times l}}{A}$
In the above equation, putting \[l = 1m\] and \[R = \rho \] this resistance is called resistivity.The ohm metre \[\left( {\Omega m} \right)\] is the unit of resistivity.The resistance of a conductor is determined by its dimensions (length and area) as well as its resistivity.
\[R = \dfrac{{\rho \times l}}{A}\]

Experiment to see which factors influence resistance:
-Consider the electric circuit illustrated in the figure, which includes a cell, an ammeter, a nichrome wire of length \[L\] (marked 1 to 4) and a plug key.

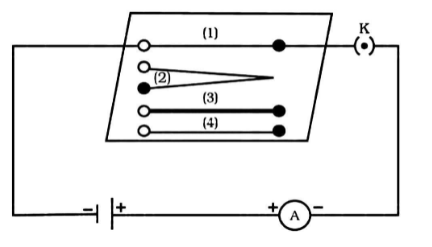
-Now, plug the key in and take note of the current ammeter reading. At point 2, replace the nichrome wire with another nichrome wire of the same thickness but twice the length \[\left( {2l} \right)\] .
-Take note of the reading once more. Change the wire for a thicker nichrome wire of the same length (marked 3). The cross-sectional area of a thicker wire is bigger.
-Note the current flowing across the circuit once more. At point 4, replace the nichrome wire with copper wire of the same length and cross-section area.
-Take note of the current value. In each scenario, note the difference in current. When the wire length is doubled, the ammeter reading falls to half of its prior value, indicating that the current through the wire is halved.
-Due to the wire's resistance, \[R\] is twice, resulting in \[R \times L\] .
-The current in the wire increases when the nichrome wire is replaced by a thicker one of the same material and length, implying that the resistance of the thicker wire (3) is lower than that of the thinner wire (1).
-This means that. When the nichrome wire is replaced with a copper wire (4) of equal length and cross-sectional area, the ammeter reads a higher current.
-This means that the resistance of copper wire is lower than that of nichrome wire of the same diameter, implying that the wire's resistance is determined by the substance it is made of.

Note: Both resistance and resistivity define how difficult it is to conduct electrical current through a material, but resistivity is an inherent feature, whereas resistance is not. This means that all pure copper wires, regardless of shape or size, have the same resistivity, yet a long, thin copper wire has a far higher resistance than a thick, short copper wire (assuming the crystalline structure has not been distorted). Every substance has its own resistivity characteristics. Rubber, for example, has a far higher resistance than copper.