Question

Effective capacitance of parallel combination of two capacitors ${{\text{C}}_1}$ and ${{\text{C}}_2}$​ is 10μF. When these capacitors are individually connected to a voltage source of 1V, the energy stored in the capacitor ${{\text{C}}_2}$ is 4 times that of ${{\text{C}}_1}$​. If these capacitors are connected in series, their effective capacitance will be:
A. 8.4μF
B. 3.2μF
C. 1.6μF
D. 4.2μF

Answer 1

Hint: Proceed the solution of this question first by finding the value of capacitors ${{\text{C}}_1}$ and ${{\text{C}}_2}$ which we can find by given conditions of parallel combination of two capacitors and energy stored condition later on using effective capacitance of series combination of two capacitor we can find the required result.

Complete Step-by-Step solution:
In the question it is given the effective capacitance of parallel combination of two capacitors ${{\text{C}}_1}$​ and ${{\text{C}}_2}$ as shown in below figure that is equal to \[{{\text{C}}_1} + {{\text{C}}_2}\] which is given by 10μF

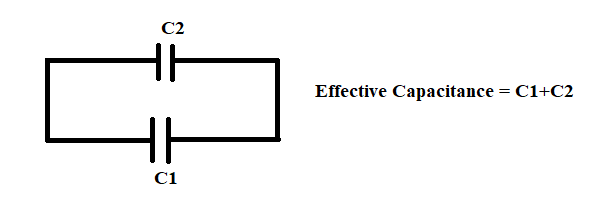
Hence ${{\text{C}}_1} + {{\text{C}}_2} = 10$ μF ...(1)
They are now connected to the same voltage source of 1V.

The energy stored in the two capacitors are given by ${{\text{E}}_1}{\text{& }}{{\text{E}}_2}$
And we know that Energy stored in any capacitor is equal to $\dfrac{1}{2}{\text{C}}{{\text{V}}^2}$
Therefore, energy stored in first and second capacitor ${{\text{E}}_1} = \dfrac{1}{2}{{\text{C}}_1}{{\text{V}}^2}{\text{ & }}{{\text{E}}_2} = \dfrac{1}{2}{{\text{C}}_2}{{\text{V}}^2}$

Given that the energy stored in the capacitor ${{\text{C}}_2}$​ is 4 times that of ${{\text{C}}_1}$​.
$ \Rightarrow {{\text{E}}_2} = {\text{4}}{{\text{E}}_1}$​
$ \Rightarrow \dfrac{1}{2}{{\text{C}}_2}{{\text{V}}^2} = 4 \times \dfrac{1}{2}{{\text{C}}_1}{{\text{V}}^2}$
On further solving
$ \Rightarrow {{\text{C}}_2} = 4{{\text{C}}_1}$
∴${{\text{C}}_2}{\text{ = 4}}{{\text{C}}_1}$………………(2)
So on putting the value of ${{\text{C}}_2}{\text{ from equation (2) in equation (1)}}$
$ \Rightarrow {{\text{C}}_1} + 4{{\text{C}}_1} = 10{\mu\text{ F}}$
$ \Rightarrow 5{{\text{C}}_1} = 10{\mu\text{F}}$
$ \Rightarrow {{\text{C}}_1} = 2{\mu\text{F}}$
Now on putting the value of \[{{\text{C}}_2}{\text{ in equation (2) }}\]
∴${{\text{C}}_2}{\text{ = 4}} \times {\text{2 = 8}}\mu {\text{F}}$

When ${{\text{C}}_1}$and ${{\text{C}}_2}$are connected in series as shown in below figure, the equivalent capacitance of the combination is given by

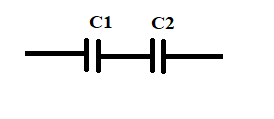
${{\text{C}}_{{\text{series}}}} = \dfrac{{{{\text{C}}_1} \times {{\text{C}}_2}}}{{{{\text{C}}_1}{\text{ + }}{{\text{C}}_2}}}$
Hence on putting the value of ${{\text{C}}_1}$ and ${{\text{C}}_2}$
${{\text{C}}_{{\text{series}}}} = \dfrac{{2 \times 8}}{{{\text{2 + 8}}}}{\mu\text{ F = }}\dfrac{{16}}{{10}}{\text{ = 1}}{.6\mu\text{ F}}$
Therefore, If capacitors ${{\text{C}}_1}$and ${{\text{C}}_2}$ are connected in series, their effective capacitance will be ${\text{1}}{.6\mu\text{F}}$

Note- In this particular question we should know that the energy stored in a capacitor is the work required to charge the capacitor, beginning with no charge on its plates. The energy is stored in the electrical field in the space between the two capacitor plates. It depends on the amount of electrical charge on capacitors plates and on the potential difference between the plates.