Questions & Answers
Question
Answers
Related Questions
How many edges are there in a cuboid?
A. 4
B. 5
C. 6
D. 12
Answer
![Verified]()
Verified
Verified
Hint: Here we can use Euler’s formula. The number of faces, the number of vertices and the number of edges of a polyhedron are related by the following formula:
Number of faces + number of vertices = number of edges + 2.
Complete step-by-step answer:
In this problem we have to find out how many edges are there in a cuboid. So, let us first draw a cuboid. We know that a cuboid is a solid figure which has six rectangular faces at right angles to each other.
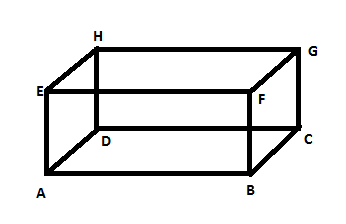
First we have to know about the vertex, edge and face of a solid figure.
A vertex is a point where two or more line segments meet. Basically a vertex is a corner. Plural of vertex is vertices. So, in this picture the vertices are $A,B,C,D,E,F,G,H$ . So there are 8 vertices in a cuboid.
A face is a single flat surface of a solid object. Like here in this figure the faces are:$ABCD,EFGH,ABFE,DCGH,ADHE,BCGF$
So, there are 6 faces in a cuboid.
An edge is a line segment between two faces. For example here the line segment between the faces $ABCD$ and $DCGH$ is $DC$ .
Now, we know the Euler’s formula:
Number of faces + number of vertices = number of edges + 2
Let us denote the number of faces by $F$.
Number of vertices by $V$.
Number of edges by $E$.
Therefore, $F+V=E+2...........(1)$
Here, the number of faces are 6. Numbers of vertices are 8. Let us put these values in (1).
$\begin{align}
& 6+8=E+2 \\
& \Rightarrow 14=E+2 \\
& \Rightarrow E=14-2 \\
& \Rightarrow E=12 \\
\end{align}$
Therefore the numbers of edges are 12.
Hence option (e) is correct.
Note: We can count the edges from the picture also. Like the edges are $AB, BC, CD, DA, EF, FG, GH, HE, AE, DH, BF, CG$. So there are 12 edges.
Number of faces + number of vertices = number of edges + 2.
Complete step-by-step answer:
In this problem we have to find out how many edges are there in a cuboid. So, let us first draw a cuboid. We know that a cuboid is a solid figure which has six rectangular faces at right angles to each other.
First we have to know about the vertex, edge and face of a solid figure.
A vertex is a point where two or more line segments meet. Basically a vertex is a corner. Plural of vertex is vertices. So, in this picture the vertices are $A,B,C,D,E,F,G,H$ . So there are 8 vertices in a cuboid.
A face is a single flat surface of a solid object. Like here in this figure the faces are:$ABCD,EFGH,ABFE,DCGH,ADHE,BCGF$
So, there are 6 faces in a cuboid.
An edge is a line segment between two faces. For example here the line segment between the faces $ABCD$ and $DCGH$ is $DC$ .
Now, we know the Euler’s formula:
Number of faces + number of vertices = number of edges + 2
Let us denote the number of faces by $F$.
Number of vertices by $V$.
Number of edges by $E$.
Therefore, $F+V=E+2...........(1)$
Here, the number of faces are 6. Numbers of vertices are 8. Let us put these values in (1).
$\begin{align}
& 6+8=E+2 \\
& \Rightarrow 14=E+2 \\
& \Rightarrow E=14-2 \\
& \Rightarrow E=12 \\
\end{align}$
Therefore the numbers of edges are 12.
Hence option (e) is correct.
Note: We can count the edges from the picture also. Like the edges are $AB, BC, CD, DA, EF, FG, GH, HE, AE, DH, BF, CG$. So there are 12 edges.
×
Sorry!, This page is not available for now to bookmark.
Like this
Liked
-
Courses-
Crash Courses 2021
-
Olympiads/NTSE/Others
-
Micro Courses
-
Vedantu Super Kids NEW
-
Reading & Spoken English -
FREEMaster Classes
-
PREMIUM1-on-1 Classes
-
Study Material
-
NCERT Solutions
-
Previous Year Papers
-
Mock Tests
-
Sample Papers
-
Reference Book Solutions
-
ICSE Solutions
-
School Syllabus
-
Revision Notes
-
Important Questions
-
Math Formula Sheets
-
-
More
Book your FREE Online counselling session
Share your contact information
Your FREE Online counselling session has been booked!
Vedantu academic counsellor will be calling you shortly for your Online Counselling session.
DONE
Please try again later
OK
NCERT Book Solutions
Reference Book Solutions
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
(Mon-Sun: 9am - 11pm IST)
Questions?
Chat with us
