Question

Eccentric angle of a point on the ellipse ${{\text{x}}^2} + 3{{\text{y}}^2} = 6$ at a distance $\sqrt 3 $​ units from the centre of the ellipse is
A .\[\dfrac{{5\pi }}{3}\]
B. \[\dfrac{\pi }{3}\]
C .\[\dfrac{{3\pi }}{4}\]
D .​\[\dfrac{{2\pi }}{3}\]

Answer 1

Hint: Proceed the solution of this question by using general parametric coordinates of any point P on ellipse which is (acosθ, bsinθ) then find the distance between center (which is origin) and point P and equalise it with the given distance in the question.

Complete step-by-step answer:
In the question, given equation of ellipse is ${{\text{x}}^2} + 3{{\text{y}}^2} = 6$
On comparing it with standard equation of ellipse which is $\dfrac{{{{\text{x}}^2}}}{{{{\text{a}}^2}}} + \dfrac{{{{\text{y}}^2}}}{{{{\text{b}}^2}}} = 1$
${\text{Equation of given ellipse is }}{{\text{x}}^2} + 3{{\text{y}}^2} = 6$
Divide by 6 on both side to convert it into standard form
$\dfrac{{{{\text{x}}^2}}}{6} + \dfrac{{{{\text{y}}^2}}}{2} = 1$
so on comparing with standard equation of ellipse
 a = $\sqrt 6 $ and b = $\sqrt 2 $
We know that, the parametric coordinate of any point P on the ellipse is
 (x=acosθ and y=bsinθ); Where θ is the eccentric angle.
So the parametric coordinate of point P is (√6cosθ, √2sinθ) ($\because $a = $\sqrt 6 $ and b = $\sqrt 2 $) Here θ be the eccentric angle of the point P.
 The center of the ellipse is at the point of origin (0,0)
It is given that

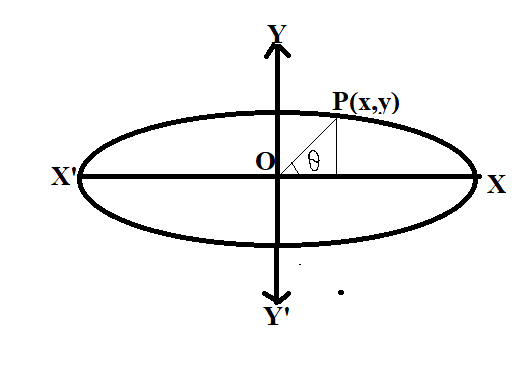
$\therefore {\text{OP = }}\sqrt 3 $
So to find length of OP,
Let the coordinates of point O $\left( {{{\text{x}}_1},{{\text{y}}_1}} \right)$ and P $\left( {{{\text{x}}_2},{{\text{y}}_2}} \right)$
So Distance between two points O and P will be = \[\sqrt {{{\left( {{{\text{x}}_2} - {{\text{x}}_1}} \right)}^2} + {{\left( {{{\text{y}}_2} - {{\text{y}}_1}} \right)}^2}} \]​
O= (0, 0), P= (√6cosθ, √2sinθ)
Here, \[{{\text{x}}_1} = 0,{{\text{y}}_1} = 0,{{\text{x}}_2} = \sqrt 6 {\text{cos}}\theta ,{{\text{y}}_2} = \sqrt 2 {\text{sin}}\theta \]
So length of side OP = $\sqrt {{{\left( {\sqrt 6 \cos \theta - 0} \right)}^2} + {{\left( {\sqrt 2 \sin \theta - 0} \right)}^2}} {\text{ = }}\sqrt {6{{\cos }^2}\theta + 2{{\sin }^2}\theta } {\text{ }}$
but It is given that ${\text{OP = }}\sqrt 3 $
 ${\text{so, }}\sqrt {6{{\cos }^2}\theta + 2{{\sin }^2}\theta } {\text{ = }}\sqrt 3 $
On squaring both side
$ \Rightarrow 6{\cos ^2}\theta + 2{\sin ^2}\theta {\text{ = 3}}$
$ \Rightarrow 6(1 - {\text{si}}{{\text{n}}^2}\theta ) + 2{\sin ^2}\theta {\text{ = 3}}$
$ \Rightarrow 6 - 6{\text{si}}{{\text{n}}^2}\theta + 2{\sin ^2}\theta {\text{ = 3}}$
$ \Rightarrow 6 - 3 = 6{\text{si}}{{\text{n}}^2}\theta - 2{\sin ^2}\theta $
$ \Rightarrow \dfrac{3}{4} = {\text{si}}{{\text{n}}^2}\theta $
$ \Rightarrow {\text{sin}}\theta = \pm \dfrac{{\sqrt 3 }}{2}$
$ \Rightarrow {\text{sin}}\theta = + \dfrac{{\sqrt 3 }}{2}{\text{ or sin}}\theta = - \dfrac{{\sqrt 3 }}{2}$
$ \Rightarrow \theta = {\sin ^{ - 1}}\left( { + \dfrac{{\sqrt 3 }}{2}{\text{ }}} \right){\text{or }}\theta = {\sin ^{ - 1}}\left( { - \dfrac{{\sqrt 3 }}{2}} \right)$
$ \Rightarrow \theta = \dfrac{\pi }{3}{\text{,}}\dfrac{{2\pi }}{3}{\text{ or }}\theta = \dfrac{{4\pi }}{3},\dfrac{{5\pi }}{3}$
$ \Rightarrow {\text{so, eccentric angle }}\theta = \dfrac{{3\pi }}{4}{\text{ }}$given in option C
Hence, Option A, B and D all are correct.

Note: In such types of particular questions, where we have assumed Parametric coordinates (trigonometric function of eccentric angles θ). In the solution we got 4 values of θ. This happens because we can assume 4 such values in each quadrant. Therefore, exactly we got 4 such values of θ in each quadrant. These 4 values of θ will also be a mirror image of each other about the x and y axis correspondingly.