Question

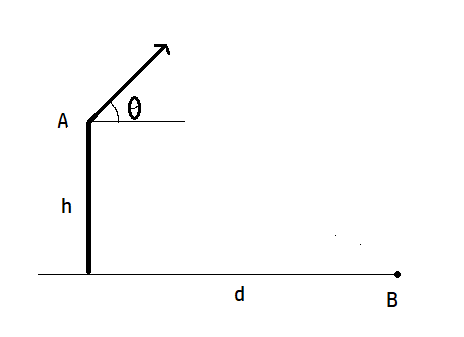
During volcanic eruptions, chunks of solid rock can be blasted out of the volcano; these projectiles are called volcanic bombs. Figure shows a cross section of Mt. Fuji, in Japan.
(a) At what initial speed would a bomb have to be ejected, at angle θ = 35 to the horizontal, from the vent at A in order to fall at the foot of the volcano at B, at vertical distance h=3.30km and horizontal distance d=9.40km? Ignore, for the moment, the effects of air on the bombs.
(b) What would be the time of flight?
(c) Would the effect of the air increase or decrease your answer in (a)?

Answer 1

Hint: after the volcanic eruption the rocks fly away making some angle with the horizontal and there is no external force acting on the system and the only force acting on the system is the force of gravity acting downwards and so there is constant acceleration in he downward direction, so, this is an example of projectile motion.

Complete step by step answer:
A- For projectile motion,
Horizontal component of velocity,
$
{{u}_{x}}=u\cos \theta \\
\implies {{u}_{x}}=u\cos 35 \\
\implies {{u}_{x}}=0.81u \\
$
Vertical component of initial velocity,
$
{{u}_{y}}=u\sin \theta \\
\implies {{u}_{y}}=u\sin 35 \\
\implies {{u}_{y}}=0.57u \\
$
There is no acceleration in horizontal direction, so horizontal velocity remains constant throughout the motion.
For projectile motion v is given by formula, \[v=\dfrac{x}{\cos \theta }\sqrt{\dfrac{g}{2(x\tan \theta -y)}}\]
Here y=-3300 m
Also, X= 9400 m
So,
 \[\begin{align}
  & v=\dfrac{9400}{\cos 35}\sqrt{\dfrac{9.8}{2(9400\times \tan 35+3300)}} \\
 & v=255.5m{{s}^{-1}} \\
\end{align}\]
B- we have found the initial velocity and now we need to find the time, we can use the formula
\[t=\dfrac{x}{{{u}_{x}}}=\dfrac{x}{v\cos 35}=\dfrac{9400}{255.5\times \cos 35}=45s\]
C-Air resistance will be negligible but to achieve the same height in presence of such resistance we need higher initial velocity.

Note:
The value of y is taken negative, although it is height and that is distance and we know distance can never be negative we had taken the origin at the point from where the rock shoots and so while using newton’s equation of motion the distance comes out to be negative