Question

Draw, wherever possible, a rough sketch of:
A quadrilateral with a rotational symmetry of order more than, but not a line symmetry.

Answer 1

Hint: The above question demands that there should be no line of symmetry in the quadrilateral drawn but it should have order of rotational symmetry more than 1. This means that the quadrilateral which we are going to draw should not have any possibility of drawing a line with respect to which the quadrilateral is symmetric. Now we are going to see how this can be done.

Complete step-by-step answer:
Thus we have to draw such a quadrilateral which satisfies both the conditions given in question. Thus the only quadrilateral which satisfies the conditions given in question are parallelograms. In parallelogram, two angles are more than \[{{90}^{\circ }}\]. So the parallelogram is drawn as shown below:-

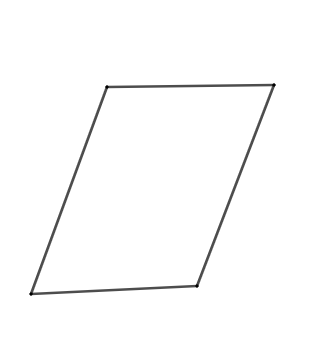
Thus, we can see that in a parallelogram, we cannot draw a line with respect to which the parallelogram is symmetric. So we can say that there is no line of symmetry in a parallelogram. Now we have to check the condition of rotational symmetry. We will now increase the angle of rotation gradually and we will check for the rotational symmetry. When the angle of rotation becomes \[{{180}^{\circ }}\] then the parallelogram becomes the same as that of the unrotated parallelogram. So, we can say that a parallelogram has rotational symmetry and the order of rotational symmetry is more than 1. Thus, the parallelogram is satisfying both the conditions given in question.

Note: We cannot draw a rhombus (a form of parallelogram) instead of the one given in question because in rhombus, there is a line of symmetry present, which violates the condition given in question.