Question

Draw, wherever possible, a rough sketch of:
A triangle with only line symmetry and no rotational symmetry order more than!

Answer 1

Hint: In the above question, we have to draw such a triangle that it has no rotational symmetry. It means that when the triangle is rotated through \[{{360}^{\circ }}\]; there should not be any angle at which the triangle is the same as that of the triangle when it is in an unrotated position. Also there should be at least a single line through which the triangle is symmetric with.

Complete step-by-step answer:
Thus, to satisfy the above condition, the triangle should be an isosceles triangle as shown below:-

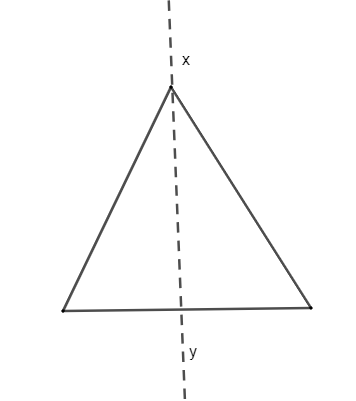
Thus, we can see that, in the above triangle, there is symmetry about the line \[x-y\]. So we can say that the \[x-y\] line is an axis of symmetry. We can say that with respect to the axis line \[x-y\], the figure is symmetric. So, we can say that the given isosceles triangle has a line of symmetry. Now, we need to check for the condition of rotational symmetry. So, we start rotating the given isosceles triangle. When it is rotated through \[{{360}^{\circ }}\], it resembles the unrotated isosceles triangle.
So, we can conclude that the order of rotational symmetry of an isosceles triangle is 1. So the isosceles triangle is satisfying both the conditions given in the question, that is it has line symmetry and no rotational symmetry.

Note: The triangle should be isosceles only. If the triangle is equilateral, then it will have both line and rotational symmetry. If the triangle is scalene, then it will have neither line nor rotational symmetry. Thus due to above conditions being failed in both the cases, the triangle should be isosceles only.