Question

Draw two direct common tangents to two congruent circles of radii 3.5 and whose distance between them is 3 cm.

Answer 1

Hint: We will start by first drawing the line segment of 3 cm. Then we will draw two circles taking end points of line segment as centres of 3.5 cm each. Then we will draw two perpendicular to the line segment then connect the end points of two perpendicular resulting in the formation of direct common tangent.
Complete step-by-step solution -
A common tangent to two circles is a straight line that touches (is a tangent to) two circles. If it crosses the interval joining the centres of the circle it is a transverse common tangent, otherwise it is a direct common tangent.
For finding direct common tangents of two circles, find the point P dividing the line joining the centre externally in the ratio of the radii. Equation of direct common tangents is:
$S{S_1} = {T_2}$ ,
Where S is the equation of one circle.
All the measurements in the figure below are in cm.

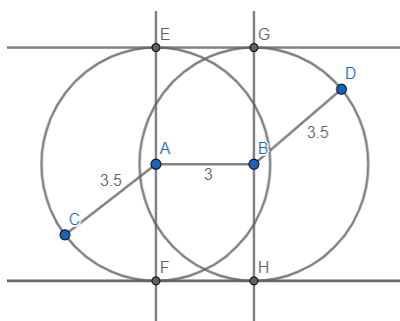
1. Draw a line segment AB of length = 3cm
2. Taking centres as point A and point B,
3. Draw two circles of radius = 3.5cm
4. Draw perpendicular EF taking base as line segment AB and passing through point A,
5. Draw perpendicular GH taking base as line segment AB and passing through point B,
6. The perpendicular drawn at A intersects circle 1 at E and F, while the perpendicular drawn at B intersects the circle 2 at G and H.
7. Join point E and point G and also join point F and point H.
8. On joining points E, G, F and H we get two lines EG and FH.
9. EG and FH are the tangents.
These are the two direct common tangents to circle 1 and circle 2.

Note: On solving this type of questions, the basic problem faced is to measure the segment correctly. A slight error in measurement can result in major error. The geometry of the figures must be perfect.