Question

Draw two circles whose radii are 4.5 cm and 3.5 cm and the distance between their centres is 10.0 cm. Find the length of the common external tangents.

Answer 1

Hint Draw the figure as given in the question. There will be two tangents in the figure, both having the same length. Draw a line parallel to AB from point C. Now triangle CDE is a right triangle because CD is a tangent and that makes angle CDE= 90 degrees. Now, apply Pythagoras to find the length of CD

Complete step-by-step answer:
We need to find the length of the tangents so for that purpose let us first draw a diagram so as to get clarity on what we need for the calculation of the length of the tangent.

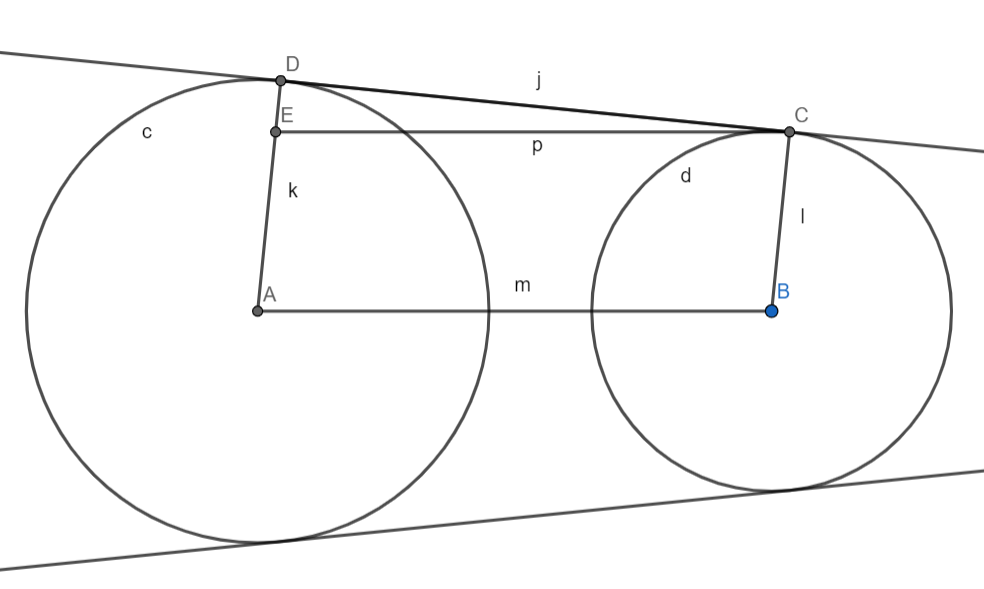
We have to find the length CD. We know that the distance between the two centres is 10 cm. and the line CE is parallel to AB so length of CE = 10 cm.


Length of DE = AD – BC = 1 cm.


Since CD is tangent to the circle so the triangle CED is a right triangle and we have to find the length of CD.


Triangle CDE is a right triangle so we apply Pythagoras theorem to find the length CD.


CD2 + DE2 = CE2.

CE2 = 102 – 12,
CE2 = 99.


So, the value of the length of the tangent is 9.94 cm.


Note: while finding out the value of tangent make sure that you have taken the sides of the triangle correctly for the Pythagoras and we have drawn the diagram correctly