Question

How do you draw the slope field of the differential equation \[{{y}^{'}}=y-x\]?

Answer 1

Hint: A slope field is a visual representation of a differential equation of the form \[\dfrac{dy}{dx}=f(x,y)\].At each sample point \[(x,y)\], there is a small line segment whose slope equals the value of \[f(x,y)\]. Slope fields allow us to analyze differential equations graphically.

Complete step by step answer:
If we have given a differential equation in x and y, we can draw a segment with \[\dfrac{dy}{dx}\] as slope at any point \[(x,y)\]. That's the slope field of the equation.
we have to substitute values of x and y into our differential equation. The result will be the value of \[{y}'\] that is the solution of our differential equation which represents the slope in that point of our function.
Consider a case \[x=2\] and \[y=2\].
Then the differential equation will be \[\Rightarrow {{y}^{'}}=y-x=2-2=0\].
This means \[slope=0\] and you'll draw a horizontal line at \[(2,2)x=y\].
It is shown in the below figure.

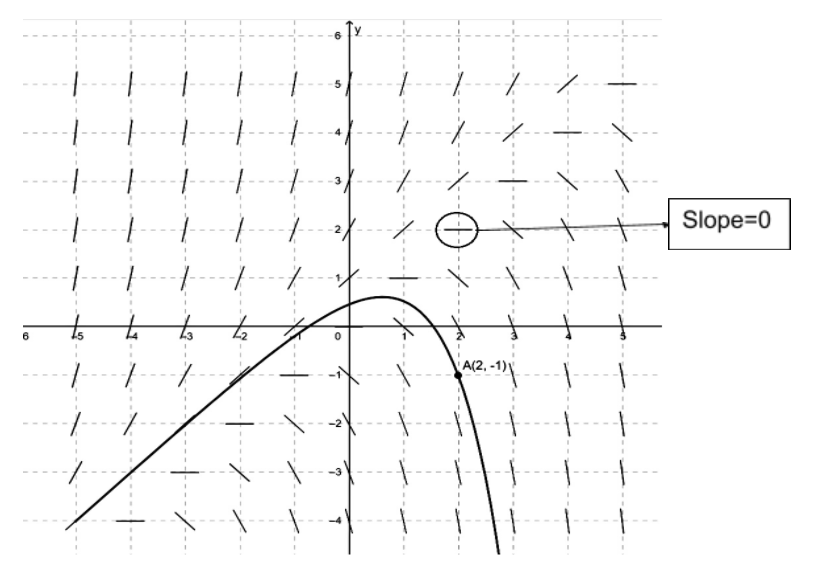
We can say that at every point where \[x=y\] has a slope equal to zero. So we draw horizontal lines on the slope field at \[x=y\].
Similarly, by taking other points and plotting their slopes at their respective points gives us the slope field graph.
In this way we can plot the slope field of any differential equation.

Note: In order to solve these types of problems, we must have enough knowledge over slope field equations, differential equations. We may use pencil and paper and draw at each point a little line with inclination representing the value calculated at that point.