Question

Draw the angle of ${{90}^{\circ }}$ using the protractor and then bisect the angle.

Answer 1

Hint: Using the protractor value marks we draw the angle of ${{90}^{\circ }}$. We draw a line of base and find the perpendicular line. Then we use a compass to find the arc of the angle and using the same arc length we find the intersecting point of the angle. We join two points to get the angle bisector.

Complete step by step answer:
We first draw the given angle of ${{90}^{\circ }}$ using the protractor.
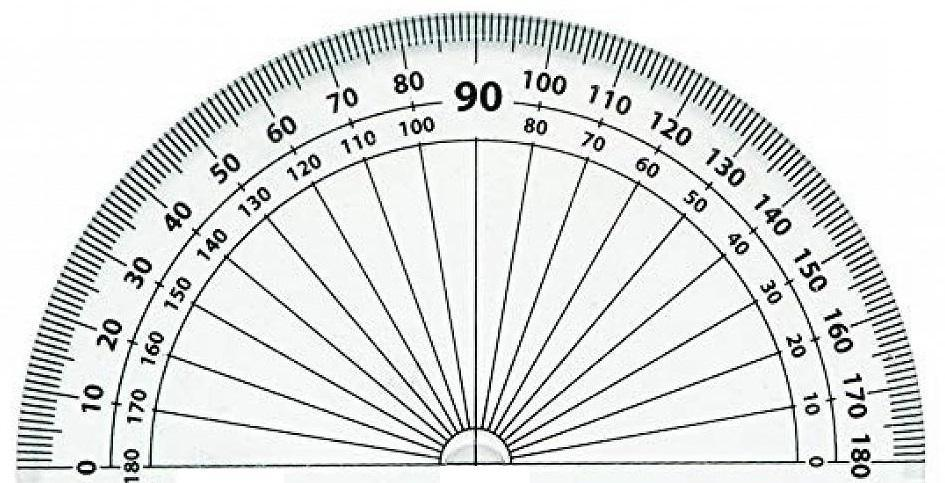
The protractor is used to establish and test angles to very close tolerances. It measures angles from ${{0}^{\circ }}$ to ${{180}^{\circ }}$ in one go. The angles are divided into unitary angles.
${{90}^{\circ }}$ mark is exactly in the middle of the instrument.

So, we first draw a line segment AB of any length.
Then we want to draw the angle of ${{90}^{\circ }}$. So, we put the base of the protractor on the line and place the fixing point on point A.
We take a point C on the 90 marks. We join A and C.
Using the protractor, we got $\angle CAB={{90}^{\circ }}$.
Now we need to divide this angle.
Now we use a compass to bisect the angle.
We take an arc of any radius on the angle which cuts the two sides on the point D and E.
Now we won’t change of the length of the arc in the compass.
Using the same length, we put it on both points D and E and take two more arc.
We need to find the intersecting points of these two arcs.
Then with join the intersecting point with point A to find the bisecting line of $\angle CAB={{90}^{\circ }}$.
So, we name the intersecting point F. AF is the angle bisector of $\angle CAB$.

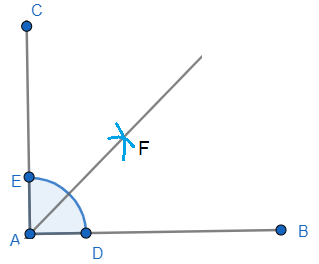
We get 2 angles which are equal which means $\angle CAF=\angle BAF=\dfrac{1}{2}\angle CAB={{45}^{\circ }}$.

Note:
Although we used a compass to draw the bisector, we can use a protractor also to find it. We know the bisector is ${{45}^{\circ }}$. So, we use the ${{45}^{\circ }}$ mark on the protractor to find the bisector. Then join the points to find the line segment. We need to remember that we can’t change the arc length in any case.