Question

Draw an angle of \[{180^ \circ }\] and divide it into four angles by bisecting the angles simultaneously.

Answer 1

Hint: Here in this question belongs to construction topic, we have to construct the four bisecting angles in the linear angle \[{180^ \circ }\], which means we have drawn four \[{45^ \circ }\] angles inside the angle \[{180^ \circ }\] by using a geometrical instruments like centimeter scale, compass with provision of fitting a pencil and protractor.

Complete step by step solution:
The bisector is a line that divides a line or an angle into two equivalent parts. The bisector of a segment always contains the midpoint of the segment.
There are two types of bisectors i.e.,
Line bisector - A line segment bisector divides the line segment into 2 equal parts. It passes through the midpoint of the line segment.
Angle bisector - An angle bisector divides an angle into equal angles.
Now, consider the given question
Draw an angle of \[{180^ \circ }\] and divide it into four angles by bisecting the angles simultaneously.
To construct the bisector of a given angle follow the below steps:
Given that, draw an angle AOB of \[{180^ \circ }\] which means it’s angle is straight angle, we want to construct its four bisecting angles.
Steps of Construction:
I.Taking ‘O’ as centre and any radius, draw an arc to intersect the lines OB and OA.
Next, take B as centres and with the same radius which is taken in 1st step, draw arcs C and take C as centre and with the same radius draw an arc E again E as centre draw an arc with same radius it comes on the point A.
II.Now, we have to draw first bisector which divides \[{180^ \circ }\] in to two equal halves i.e., \[{90^0}\] by taking E and C as centre with the same radius draw an arc in the upwards direction the two arcs are intersect name as D draw a line from the point O to D it makes an angle \[{90^0}\] each.
III.Now, again draw a bisector which divides \[{90^0}\] in to two equal halves i.e., \[{45^0}\], by taking B and D as centre with the same radius draw an arc in the upwards direction the two arcs are intersect name as C draw a line from the point O to C it makes an angle \[{45^0}\] each.
IV.Similarly draw a bisector for remaining angle \[{90^0}\], by taking A and D as centre with the same radius draw an arc in the upwards direction the two arcs are intersect name as E draw a line from the point O to E it makes an angle \[{45^0}\] each.
The construction of four bisectors of angle \[{180^0}\] is

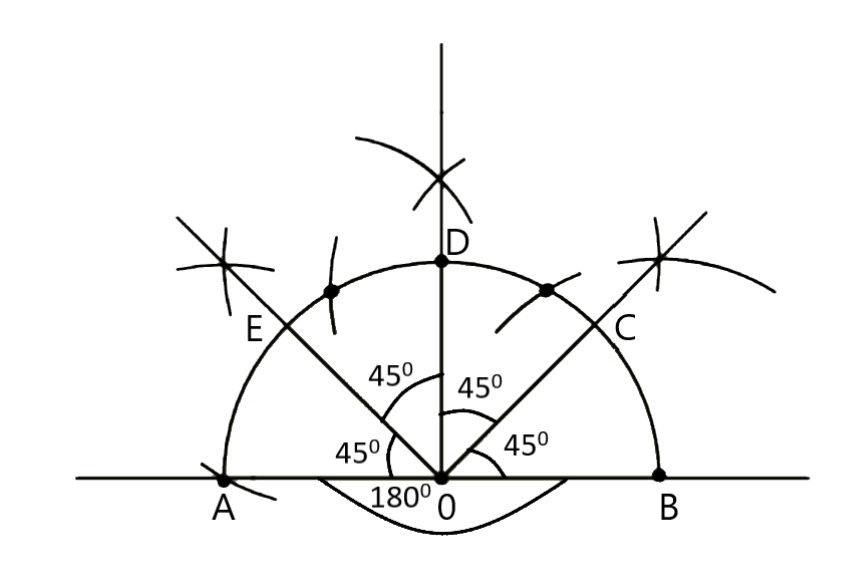
Note: When doing construction handling the instruments carefully, remember when making an arc between an angle the radius will be the same which cannot be altered. If we can verify the construction easily i.e., The given angle is \[{180^0}\], the four equal parts of \[{180^0}\] is \[\dfrac{{{{180}^0}}}{4} = {45^0}\], the four bisector should be a angle of \[{45^0}\] we can measure the angle of each bisector directly by using a instrument called protractor.