Question

Draw a Venn diagram, showing sub-set relations of the following sets.
$A = \left\{ {2,4} \right\}$
$B = \left\{ {x|x = {2^n},n \leqslant 5,n \in N} \right\}$
$C = \left\{ {x|x{\text{ is an even natural number}} \leqslant 16} \right\}$

Answer 1

Hint: Here, we will first convert all the sets to roster form. Then, by drawing circles or ovals, we will be able to draw the Venn diagram showing the relationship between the given sets. In mathematics, a set is defined as an organized collection of objects or elements that can be represented in set-builder form as well as in roaster form.

Complete step-by-step answer:
First, we will convert the sets which are given in set-builder form to the roster form.
Here, set $A$ is already in roster form.
Now, set $B = \left\{ {x|x = {2^n},n \leqslant 5,n \in N} \right\}$
This implies that $n$ is any natural number which is less than equal to 5.
As we know, natural numbers are those numbers which are greater than equal to 1.
Hence, the values which $n$ can take, will be: $1,2,3,4,5$ satisfying $n \leqslant 5,n \in N$
Now, it is given that $x = {2^n}$
Hence, substituting $n = 1,2,3,4,5$ one-by-one, we will get the possible values of $x$ as:
$x = {2^1},{2^2},{2^3},{2^4},{2^5}$
$ \Rightarrow x = 2,4,8,16,32$
Therefore, set $B$ in roster form, can be written as:
$B = \left\{ {2,4,8,16,32} \right\}$
Now, we will convert set $C = \left\{ {x|x{\text{ is an even natural number}} \leqslant 16} \right\}$ into roster form.
This implies that $x$ is any even natural number that is less than equal to 16.
As we know, natural numbers are those numbers which are greater than equal to 1 and even numbers are those numbers which are divisible by 2.
Hence, the values which $x$ can take, will be: $2,4,6,8,10,12,14,16$ satisfying $x \leqslant 16$, where $x$ is an even natural number.
Therefore, set $C$ in roster form, can be written as:
$C = \left\{ {2,4,6,8,10,12,14,16} \right\}$
Hence, in roster form, we get the three sets as:
$A = \left\{ {2,4} \right\}$
$B = \left\{ {2,4,8,16,32} \right\}$
$C = \left\{ {2,4,6,8,10,12,14,16} \right\}$
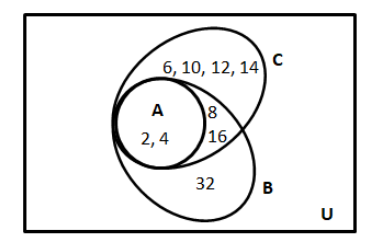
Now, we are required to draw a Venn diagram, showing sub-set relations of these three sets.
Thus, the required Venn diagram is:

Note: A Venn diagram is a pictorial representation of the relationships between sets. It is usually represented by drawing circles or ovals. In mathematics, a set consists of a list of elements or numbers which are enclosed in curly brackets. The set-builder form of a set is used to represent an equation, an inequality, or the numbers which have some kind of relation. This is also used to represent an infinite number of elements.
The roster form is the simpler form of a set. In this form, we separate the numbers with the help of commas and they are enclosed again, in brackets.