Question

Draw a triangular prism and verify Euler’s Formula.

Answer 1

Hint:
We have to verify Euler’s Formula , for this we have to show that the number of faces, vertices, and edges of any polyhedron. It states that the sum of the number of faces and vertices is equal to the two more than the number of edges. Mathematically we can write , \[F{\text{ }} + {\text{ }}V{\text{ }} = {\text{ }}E{\text{ }} + {\text{ }}2,\] where $F$ is that the number of faces, \[V\] the number of vertices, and $E$ the number of edges.

Complete step by step solution:
Let us consider a triangular prism given below ,

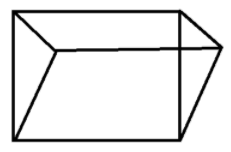
Now recall Euler’s formula, Either of two important mathematical theorems of Euler. the primary may be a topological invariance relating the number of faces, vertices, and edges of any polyhedron. It states that the sum of the number of faces and vertices is equal to the two more than the number of edges. Mathematically we can write , \[F{\text{ }} + {\text{ }}V{\text{ }} = {\text{ }}E{\text{ }} + {\text{ }}2,\] where $F$ is that the number of faces, \[V\] the number of vertices, and $E$ the number of edges. A cube, for instance, has six faces, eight vertices, and twelve edges, and satisfies this formula.
Therefore, consider \[F{\text{ }} + {\text{ }}V{\text{ }} = {\text{ }}E{\text{ }} + {\text{ }}2,\]
Here, In this triangular prism ,
The number of faces , $F = 5............(1)$
The number of vertices , $V = 6...............(2)$
Now, add $(1),(2)$ equations , we will get ,
$ \Rightarrow F + V = 5 + 6 = 11................(3)$
And the number of edges , $E = 9$
$ \Rightarrow E + 2 = 9 + 2 = 11...............(4)$
After comparing $(3)$ and $(4)$ , we can say that ,
Euler’s Formula is verified.

Note:
Questions similar in nature as that of above can be approached in a similar manner and we can solve it easily. For solving this type of question, we have to consider the polyhedron , so that we can count its edges, vertices and faces.