Question

Draw a square of area $ 13 $ square centimetres ?

Answer 1

Hint: Here in this question, we have to draw a square whose area is given to us as $ 13 $ square centimetres. To find the area of a square, we have a standard formula $ Area = {\left( {Side} \right)^2} $ . We know the value of the area of the square as it is provided to us in the problem itself. We substitute the known values and determine the length of the side of the square using the formula. $ Area = {\left( {Side} \right)^2} $

Complete step-by-step answer:
A square is a two dimensional shape with four equal sides. So, it is a quadrilateral with all of the sides being equal and each angle being a right angle.
To determine the area of a square, we have standard formula $ A = {\left( {Side} \right)^2} $ where A represents the area of the square. The side of a square is the line segment which joins two consecutive vertices of a square. The side of a square is often denoted as ‘S’ or ‘s’. The unit for the area is square units. In the given question, we are given the area of the square in square centimetres. So, we get the length of the sides of the square using the formula in the unit centimetres.
To find the length of the side of the square, we use formula $ A = {\left( {Side} \right)^2} $ .
By substituting the value of the area of the square, we get,
 $ \Rightarrow 13\,c{m^2} = {\left( {Side} \right)^2} $
Now, taking square root on both sides of the equation, we get,
 $ \Rightarrow \left( {Side} \right) = \sqrt {13\,c{m^2}} $
As we know that the length of the side of the square cannot be negative. So, we take only the positive square root of the area of the square in order to calculate the length of the side of the square. So, we get,
 $ \Rightarrow \left( {Side} \right) = \sqrt {13\,} cm $
Now that we know that the length of the side of the square whose area is given to us as $ 13 $ square centimetres is $ \sqrt {13} $ centimetres. So, now we can draw the figure of a square whose length of side is $ \sqrt {13} \,cm $ and area of the square is $ 13\,c{m^2} $ .
So, we get,

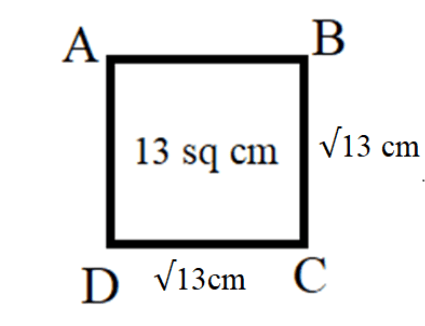
Note: Generally the area is the region occupied by the thing. The area of a square is defined as the region occupied by the quadrilateral region. It can be determined by using formula $ A = {s^2} $ where s represents the side of the square and A denotes the area of the square.