Question

Draw a rough diagram of two angles such that they have four points in common.

Answer 1

Hint: First draw an acute angle ABC with vertex at B and AB and BC as its sides. Now, take another point D outside the angle ABC and join BD to form the second angle ABD. From the figure, you will see that only A and B are the common points. So, it is impossible to draw two angles such that they have four points in common.

Complete step-by-step solution -
In this question, we need to draw a rough diagram of two angles such that they have four points in common.
Let us first define what an angle actually is.
In plane geometry, an angle is the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex of the angle.
Now, first we will draw an angle ABC with vertex at B and AB and BC as its sides.

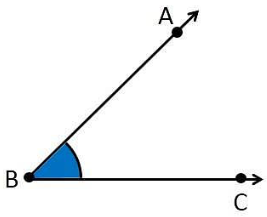
Here, we have three points: B as the vertex and A and C on the sides of the angle ABC.
Now, we will take another point D outside the angle ABC and join BD to form the second angle ABD.

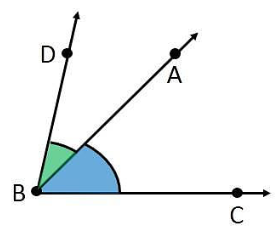
Now, from this new figure, we can see that the angles ABC and ABD have only two points common. These two points are point B, which is the vertex of both the angles and point A which lies on the common side of the angles.
Since, we can have only one endpoint, hence it is impossible to draw two angles such that they have four points in common.
This is our final answer.

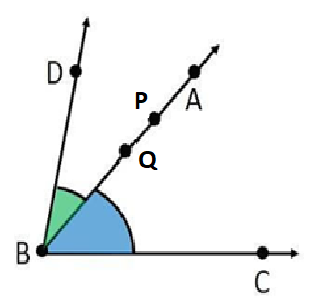
Note: Another different approach to this problem can be: We draw the same figure as before for the two angles. Now we know that a ray has an infinite number of points. So, on the common side, we choose 2 additional points P and Q which are common to both the angles. In this way, two angles can have four common points.