Question

Draw a real velocity versus time graph for Mars.

Answer 1

Hint: According to Kepler’s second law of planetary motion; the areal velocity of the planet remains constant. Recall the expression for Kepler’s second law of planetary motion. Mars or every planet in the solar system orbits at higher speed when it is closest to the sun and it orbits at lower speed when it is farthest from the sun. therefore, the angular momentum remains constant.

Complete answer:
The answer of the question is based on Kepler’s second law of planetary motion.We have according to Kepler’s second law of planetary motion; the areal velocity of the planet remains constant. That is the imaginary line joining the planet to the sun sweeps out equal areas in equal intervals of time. We have the expression for the Kepler’s second law of planetary motion,
\[\dfrac{{dA}}{{dt}} = \dfrac{L}{{2m}}\]
Here, \[\dfrac{{dA}}{{dt}}\] is the rate of change of area, L is the angular momentum and m is the mass of Mars.
We know that the angular momentum is the product of radius of circular motion and the linear or orbital velocity of the planet. Therefore,
\[L = \vec r \times \vec v\]
As we know, Mars or every planet in the solar system orbits at higher speed when it is closest to the sun and it orbits at lower speed when it is farthest from the sun. Therefore, the product \[\vec r \times \vec v\] remains the same. Thus, the angular momentum of the planet around the sun remains constant.

So, we can say that the areal velocity \[\dfrac{{dA}}{{dt}}\] does not change with time t and therefore, the graph between areal velocity and time will be parallel to the time axis as shown in the figure below.

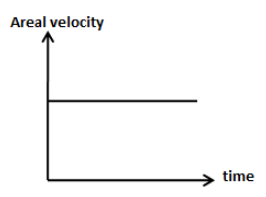
Note:Students don’t need to stretch the answer towards the angular momentum of the planet. The areal velocity remains constant means \[\dfrac{{dA}}{{dt}} = {\text{constant}}\]. Therefore, students can easily interpret that the areal velocity versus time graph shows no change in areal velocity with respect to time t.