
Draw a pie chart for the following data:
Team of expenditure Food Health Clothing Education Saving Amount spent in Rupees 3750 1875 1875 1200 7500
| Team of expenditure | Food | Health | Clothing | Education | Saving |
| Amount spent in Rupees | 3750 | 1875 | 1875 | 1200 | 7500 |
Answer
506.6k+ views
Hint: We have been given data for which we have to draw a pie chart. For this, we will first calculate the fraction of expenditure of all the teams given by $\dfrac{\text{Amount spent on the required team}}{\text{Total amount spent on all the teams}}$ then we will calculate the fraction of angle of each team out of ${{360}^{\circ }}$ by multiplying the fraction of expenditure of each team by ${{360}^{\circ }}$. Then when we finally get all the required angles, we can draw the pie chart by drawing a circle through a compass and then by drawing portions of these angles by the help of a protractor.
Complete step-by-step answer:
We here have been given the following data and we have to draw its pie chart:
For this, we will first calculate the fraction of each team of expenditure.
We know that fraction of expenditure of each team is calculated as: $\dfrac{\text{Amount spent on the required team}}{\text{Total amount spent on all the teams}}$
We will now first calculate the total amount spent on all the teams.
Now, the total amount spent in rupees on all the teams is:
\[\begin{align}
& 3750+1875+1875+1200+7500 \\
& \Rightarrow \text{Rs}\text{. }16200 \\
\end{align}\]
Now, we will calculate the fraction of expenditure of each team.
Fraction of expenditure of team food is given as:
$\begin{align}
& \dfrac{\text{Amount spent on team food}}{\text{Total amount spent on all the teams}} \\
& \Rightarrow \dfrac{3750}{16200} \\
& \Rightarrow \dfrac{25}{108} \\
\end{align}$
Fraction of expenditure of team health is given as:
$\begin{align}
& \dfrac{\text{Amount spent on team health}}{\text{Total amount spent on all the teams}} \\
& \Rightarrow \dfrac{1875}{16200} \\
& \Rightarrow \dfrac{25}{216} \\
\end{align}$
Fraction of expenditure of team clothing is given as:
$\begin{align}
& \dfrac{\text{Amount spent on team clothing}}{\text{Total amount spent on all the teams}} \\
& \Rightarrow \dfrac{1875}{16200} \\
& \Rightarrow \dfrac{25}{216} \\
\end{align}$
Fraction of expenditure of team education is given as:
$\begin{align}
& \dfrac{\text{Amount spent on team education}}{\text{Total amount spent on all the teams}} \\
& \Rightarrow \dfrac{1200}{16200} \\
& \Rightarrow \dfrac{2}{27} \\
\end{align}$
Fraction of expenditure of team saving is given as:
$\begin{align}
& \dfrac{\text{Amount spent on team savings}}{\text{Total amount spent on all the teams}} \\
& \Rightarrow \dfrac{7500}{16200} \\
& \Rightarrow \dfrac{25}{54} \\
\end{align}$
Now that we have all the fractions of expenditures on all the teams, we can calculate the fraction of their angles out of the complete angle.
Now, we know that the complete angle of a pie chart is equal to ${{360}^{\circ }}$ and the fraction of angle of each team of expenditure is given as:
$\text{Fraction of expenditure on the required team}\times {{360}^{\circ }}$
Thus, the angle of each team of expenditure is given in a tabular form as:
Now, that we have all the required angles, we can draw a circle through a compass and by the help of a protractor, we can draw these angles inside the circle and label them as they are given to us.
Hence, we will get our pie chart as:
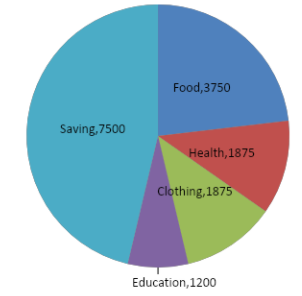
Thus, we have our required pie chart.
Note: We should make sure that when we calculate the fractions of the angles of each team, the sum of all the angles should be equal to ${{360}^{\circ }}$. It is a check if the fractions that we calculated are correct or not. Here also, if we check the sum of all the angles we will get:
${{83.34}^{\circ }}+{{41.66}^{\circ }}+{{41.66}^{\circ }}+{{26.67}^{\circ }}+{{166.67}^{\circ }}={{360}^{\circ }}$
Thus, our calculations are correct.
Complete step-by-step answer:
We here have been given the following data and we have to draw its pie chart:
| Team of expenditure | Food | Health | Clothing | Education | Saving |
| Amount spent in Rupees | 3750 | 1875 | 1875 | 1200 | 7500 |
For this, we will first calculate the fraction of each team of expenditure.
We know that fraction of expenditure of each team is calculated as: $\dfrac{\text{Amount spent on the required team}}{\text{Total amount spent on all the teams}}$
We will now first calculate the total amount spent on all the teams.
Now, the total amount spent in rupees on all the teams is:
\[\begin{align}
& 3750+1875+1875+1200+7500 \\
& \Rightarrow \text{Rs}\text{. }16200 \\
\end{align}\]
Now, we will calculate the fraction of expenditure of each team.
Fraction of expenditure of team food is given as:
$\begin{align}
& \dfrac{\text{Amount spent on team food}}{\text{Total amount spent on all the teams}} \\
& \Rightarrow \dfrac{3750}{16200} \\
& \Rightarrow \dfrac{25}{108} \\
\end{align}$
Fraction of expenditure of team health is given as:
$\begin{align}
& \dfrac{\text{Amount spent on team health}}{\text{Total amount spent on all the teams}} \\
& \Rightarrow \dfrac{1875}{16200} \\
& \Rightarrow \dfrac{25}{216} \\
\end{align}$
Fraction of expenditure of team clothing is given as:
$\begin{align}
& \dfrac{\text{Amount spent on team clothing}}{\text{Total amount spent on all the teams}} \\
& \Rightarrow \dfrac{1875}{16200} \\
& \Rightarrow \dfrac{25}{216} \\
\end{align}$
Fraction of expenditure of team education is given as:
$\begin{align}
& \dfrac{\text{Amount spent on team education}}{\text{Total amount spent on all the teams}} \\
& \Rightarrow \dfrac{1200}{16200} \\
& \Rightarrow \dfrac{2}{27} \\
\end{align}$
Fraction of expenditure of team saving is given as:
$\begin{align}
& \dfrac{\text{Amount spent on team savings}}{\text{Total amount spent on all the teams}} \\
& \Rightarrow \dfrac{7500}{16200} \\
& \Rightarrow \dfrac{25}{54} \\
\end{align}$
Now that we have all the fractions of expenditures on all the teams, we can calculate the fraction of their angles out of the complete angle.
Now, we know that the complete angle of a pie chart is equal to ${{360}^{\circ }}$ and the fraction of angle of each team of expenditure is given as:
$\text{Fraction of expenditure on the required team}\times {{360}^{\circ }}$
Thus, the angle of each team of expenditure is given in a tabular form as:
| Team of expenditure | Angle out of the complete angle of each team |
| Food | $\dfrac{25}{108}\times {{360}^{\circ }}={{83.34}^{\circ }}$ |
| Health | $\dfrac{25}{216}\times {{360}^{\circ }}={{41.66}^{\circ }}$ |
| Clothing | $\dfrac{25}{216}\times {{360}^{\circ }}={{41.66}^{\circ }}$ |
| Education | \[~\dfrac{2}{27}\times {{360}^{\circ }}={{26.67}^{\circ }}\] |
| Saving | $\dfrac{25}{54}\times {{360}^{\circ }}={{166.67}^{\circ }}$ |
Now, that we have all the required angles, we can draw a circle through a compass and by the help of a protractor, we can draw these angles inside the circle and label them as they are given to us.
Hence, we will get our pie chart as:

Thus, we have our required pie chart.
Note: We should make sure that when we calculate the fractions of the angles of each team, the sum of all the angles should be equal to ${{360}^{\circ }}$. It is a check if the fractions that we calculated are correct or not. Here also, if we check the sum of all the angles we will get:
${{83.34}^{\circ }}+{{41.66}^{\circ }}+{{41.66}^{\circ }}+{{26.67}^{\circ }}+{{166.67}^{\circ }}={{360}^{\circ }}$
Thus, our calculations are correct.
Recently Updated Pages
Master Class 8 Maths: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 7 Maths: Engaging Questions & Answers for Success

Class 7 Question and Answer - Your Ultimate Solutions Guide

Master Class 6 Maths: Engaging Questions & Answers for Success

Class 6 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

Which animal has three hearts class 11 biology CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




