Question

Draw a line segment \[AB = 6.2\] cm Mark a point \[P\], in \[AB\] such that \[BP = 4\] cm through point \[P\] draw perpendicular to \[AB\].

Answer 1

Hint: Here in this question belongs to construction topic, we have to construct the perpendicular line at point P on the line AB of length 6.2 cm, where point P lies 4cm from the point B in the line AB by using a geometrical instruments like centimeter scale, compass with provision of fitting a pencil and protractor.

Complete step by step solution:
Perpendicular lines are defined as two lines that meet or intersect each other at right angles (\[{90^ \circ }\]).
Now, consider the given question
Draw a line segment \[AB = 6.2\] cm Mark a point \[P\], in \[AB\] such that \[BP = 4\] cm through point \[P\] draw perpendicular to \[AB\].
To construct the perpendicular line follow the below steps:.
Steps of Construction:
I.Draw a line segment \[AB = 6.2\] cm
II.Take point 'B' as centre and radius 4cm construct an arc ‘P’ on line segment AB.
III.With P as centre and some radius draw arc meeting AB at the points C and D.
IV.With C, D as centres and equal radii [each is more than half of CD] draw two arcs, meeting each other at the point O.
V.Join OP. Then OP is perpendicular for line AB and it makes an angle \[{90^ \circ }\].
The construction of perpendicular line is

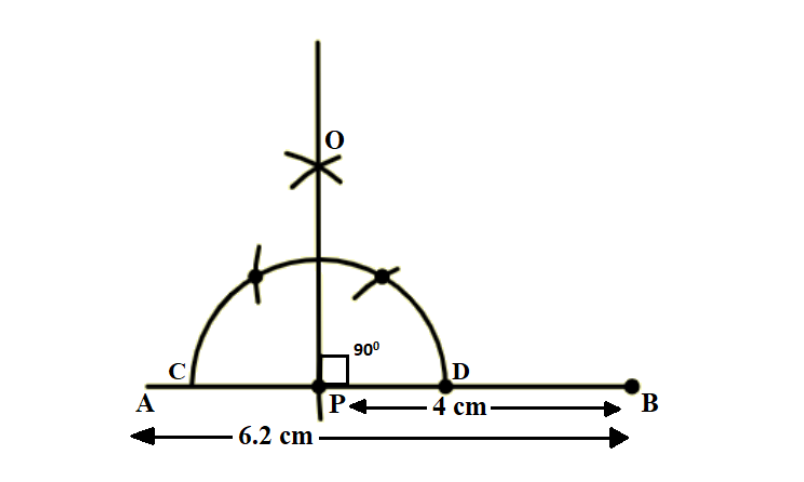
Note: When doing construction handling the instruments carefully, remember when making an arc between an angle the radius will be the same which cannot be alter and perpendicular is a line that makes an angle of \[{90^ \circ }\] with another line. \[{90^ \circ }\] is also called a right angle and is marked by a little square between two perpendicular lines otherwise the two lines intersect at a right angle, and hence, are said to be perpendicular to each other. If we can verify the construction easily by measuring the angle using an instrument called a protractor.