Question

Draw a labelled ray diagram of an image formed by a refracting telescope with the final image formed at infinity. Derive an expression for its magnifying power with the final image.

Answer 1

Hint:
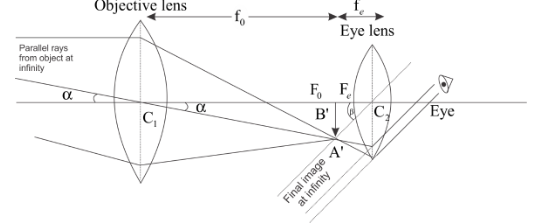
In the above question, the ray diagram of the image formed by a refracting telescope with the final image formed at infinity. The image formed will be virtual and inverted as shown in figure below.

Complete step by step answer:
Keeping the laws in mind one can approach such a question. The ray diagram is shown in the figure below.

Here in the diagram, we can see the terms explained as \[{{\text{f}}_{\text{0}}}\] is the focal length of the object and \[{{\text{f}}_{\text{e}}}\] is the focal length of the eye.
The magnifying power of a telescope is defined by the help of angle which an image subtends on the eye, in this case we have taken it to be $\beta $ to the angle subtended by the object on eye$\alpha $.
So, the magnification (m) of telescope is
$m = \left( { - \dfrac{\beta }{\alpha }} \right)$
Now, one should know the relationship of these angels in terms of length of image.
$\tan \left( \beta \right) = \dfrac{{{A'}{B'}}}{{{f_e}}}$ …………. (1)
Then,
$\tan \left( \alpha \right) = \dfrac{{{A'}{B'}}}{{{f_o}}}$ …………… (2)
Now since these angles are very small so we can take the following assumption

$
  \tan \left( \alpha \right) \approx \alpha \\
  \tan \left( \beta \right) \approx \beta \\
 $

Now, on equating (1) and (2) we get,
$\dfrac{\beta }{\alpha } = \dfrac{{{f_o}}}{{{f_e}}}$
Therefore, the magnification (m) is
$m = \left( { - \dfrac{{{f_o}}}{{{f_e}}}} \right)$

Note:
The negative magnification of the telescope indicates that the image formed is inverted whereas, the virtual image is upright, and magnification is positive. The divergence of the rays on the far side is due to the objects being kept closer to the converging lens and to get the position of the image we use extrapolation of the lines as shown by dotted lines.