Question

Draw a circuit diagram of a P-N-P transistor to obtain characteristics curves in common base configuration. Establish the relations between current amplification factors in a transistor in common base and common emitter configuration.

Answer 1

Hint:
First, we draw a diagram of a N-P-N transistor with a common base between emitter and collector. Then describe the input and output characteristics with the help of graphs. Generate the relationship between current amplification factor in common base and common emitter position.

Complete step by step solution:
In N-P-N transistors the base terminal is common between the input and the output terminals of the transistor. Here the emitter works as the input terminal, collector as the output terminal.

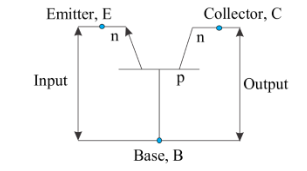
Input Characteristics:
The input characteristics of the transistor is obtained from the input current $({I_E})$ and input voltage $({V_{BE}})$.Here in this figure the output voltage $({V_{BE}})$ is kept constant and in this configuration the input voltage $({V_{BE}})$ is varied gradually and simultaneously the input current $({I_E})$ is noted down and we get this type of characteristics curve.

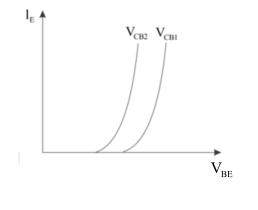Input Characteristics curve
Output Characteristics:
In the output characteristics the input current $({I_E})$ is kept constant and then the output voltage $({V_{CB}})$ is increased gradually. Thus for that variation the output current ${I_C}$ is recorded and this curve is obtained.

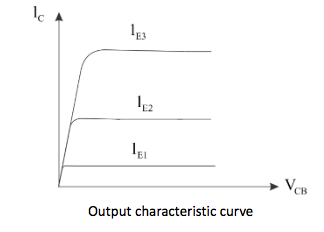
Output characteristic curve

The current amplification factor of a transistor in common base configuration is the ratio of output current $({I_C})$ to the input current $({I_E})$. It is denoted by $\alpha $.
$\alpha = \dfrac{{{I_C}}}{{{I_E}}}$.
In common emitter configuration the input current is the base current $({I_B})$ and output current is collector current$({I_C})$.
So the current amplification factor in common emitter configuration is $\beta = \dfrac{{{I_C}}}{{{I_B}}}$.
We know that ${I_E} = {I_C} + {I_B}$
So, $\beta = \dfrac{{{I_C}}}{{{I_E} - {I_C}}}$
Dividing by ${I_E}$ We get
$
  \beta = \dfrac{{\dfrac{{{I_C}}}{{{I_E}}}}}{{1 - \dfrac{{{I_C}}}{{{I_E}}}}} \\
   = > \beta = \dfrac{\alpha }{{1 - \alpha }} \\
 $
This is the relationship between $\alpha $ and $\beta $.

NoteThe significance of the relation between current amplification factors in a transistor in common base and common emitter configuration indicates that, when $\alpha $ reaches unity, then the value of $\beta $ reaches to infinity. This conclusion shows that the current gain in a common emitter configuration is very high.