Question

Draw a circle with the help of a bangle and take a point outside the circle. Construct the pair of tangents from this point to the circle.

Answer 1

Hint: Here first we need to find the center of the circle by using two non-parallel chords and then from the center we need to draw a perpendicular bisector outside the circle and then finally draw the two tangents touching the circle using it.

Complete step-by-step solution:
Here first we will draw a circle with the help of a bangle with any arbitrary radius as stated in the question. Then we need to draw non parallel chords AB and CD inside the circle in order to find the center of the circle.

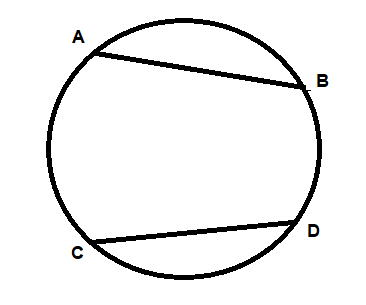
Now we will draw perpendicular bisectors of chords AB and CD by making arcs by taking more than half of the length of the chord as radius.
We know that perpendicular bisectors of the chords pass through the center of a circle.
So first taking A as the center and radius as more than half of the length of the chord AB, we need to make arcs above and below the chord and then repeat the same process by taking B as the center.
Similarly, taking C as the center and radius as more than half of the length of the chord CD, we need to make arcs above and below the chord and then repeat the same process by taking B as the center.
Now the intersection point of both the perpendicular bisectors will be the center of the circle. Mark the center as O.

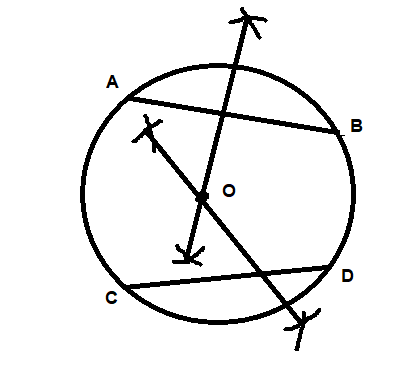
Now, we need to draw the tangents to the circle with center O.
Mark a point P outside the circle as shown below.

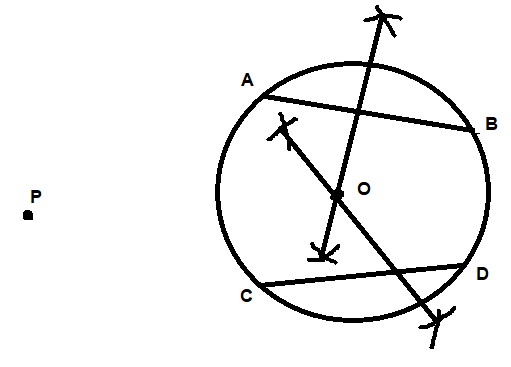
Now join O to P and make a perpendicular bisector of the line segment PO so formed and mark the intersection point as S which is the mid- point of PO.
Taking P as the center and radius as more than half of the length of the line segment PO, we need to make arcs above and below the chord and then repeat the same process by taking O as the center.

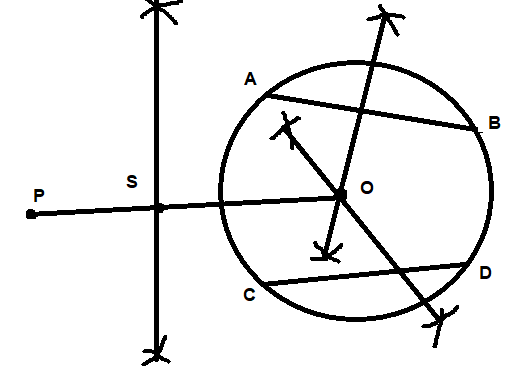
Now, take S as the center and SO as the radius and draw a circle and mark the points where the new circle intersects the old circle as Q and R.
Then join PQ and PR to get the tangents.

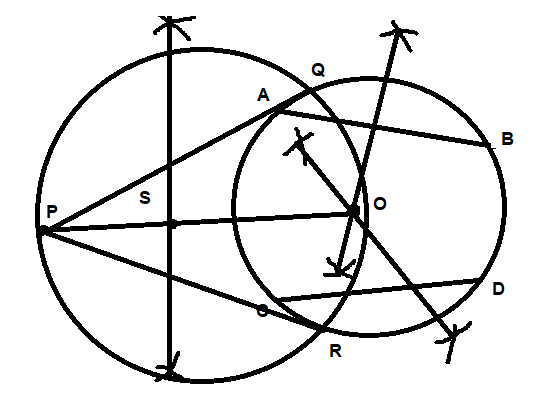
Hence PQ and PR are required tangents.

Note: Many students make mistakes while taking the radius when we have to construct arcs on points of chords, keep in mind we take radius slightly more than half and then draw arcs. Also, when joining any two points, use scale and pencil to draw straight lines. We can check the angles made by perpendicular bisectors are right angles or not using a protractor.