Question

Draw a circle with center O and radius 3.5 cm. Take a horizontal diameter. Extend it to both sides to point P and Q such that OP=OQ=7cm. Draw tangents PA and QB one above the diameter and the other below the diameter. Is $PA||PQ$.

Answer 1

Hint – Draw the diagrammatic representation using the information provided in the question. Use the property that if tangents are drawn from an external point onto a circle then the tangent makes a 90 degrees angle with the diameter and the point of contact.
Complete step-by-step answer:
Steps of construction:
$\left( 1 \right)$ Draw a circle of radius 3.5cm with center O.

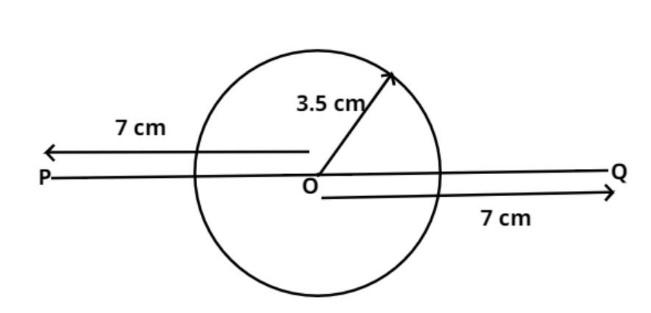
$\left( 2 \right)$ Extending the diameter from both the sides such that it meets P and Q in a way that OP=OQ=7cm.

$\left( 3 \right)$ Draw tangents from P and Q such that the tangents meet the circle on either side at A or B as shown in figure.

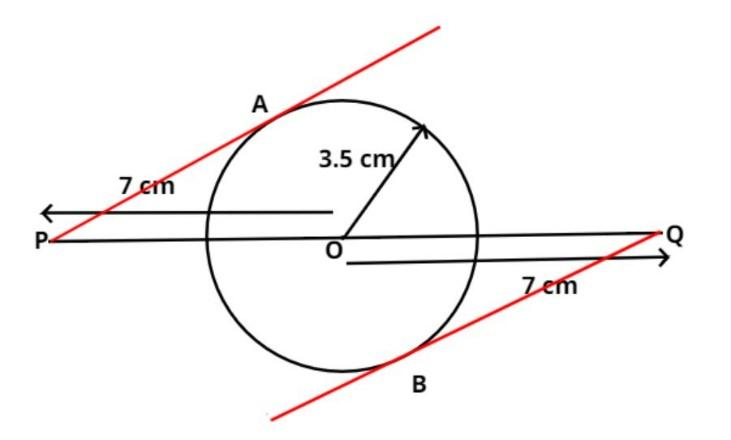
Now as we know that according to property of circle that from an external point if a tangent is drawn than the tangent makes an angle 90 degree with the radius of the circle so join point OA and OB we have,

$ \Rightarrow \angle OAP = \angle OBQ = {90^\circ}$
Now in triangle OAP and OBQ we have,
OA = OB (radius of circle)
OP = OQ = 7 cm (given)
$\angle OAP = \angle OBQ = {90^\circ}$
Therefore the triangles OAP and OBQ are similar.
Therefore the triangles OAP and OBQ are similar to each other.
Therefore sides PA and BQ are parallel to each other.
So this is the required answer.

Note – Solving such problems requires the use of CPCT that is corresponding parts of congruent triangles. CPCT is always used only when the two triangles are proved similar, there are certain criteria through which triangles can be proved similar like SSS, ASA, AAA or AAS.