Question

Draw a circle with center at point Draw its chord AB and CD such that AB is not parallel to CD. Draw the perpendicular bisector of AB and CD. At what point do they intersect?

Answer 1

Hint: Before attempting this question, one should have prior knowledge about the construction and also remember that draw chords AB and CD such that there is any possible point where both line can intersect each other which makes these chords non-parallel to each other, use this information to approach the solution.

Complete step-by-step answer:
Do stepwise construction of the question to reach to the point where they intersect.
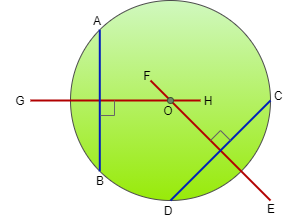
Now we have a circle centered at point O and it has two chords AB and CD such that both are non-parallel to each other.
So, let’s do it step by step.
Step 1: Draw a circle of any radius using compass and mark its center at O.
Step 2: Draw any two chords in that circle and name them AB and CD, such that they are non-parallel.
Step 3: Now take the center as B now take any radius (more than half of AB is recommended), draw two arcs, one on each side (left and right side) of the chord AB, name these arcs as G and H.
Step 4: Now with center at A and taking the same radius as taken in previous step draw two arcs, one of each side (left and right) of chord AB, cutting the previous arc G and H respectively.
Step 5: Draw a straight-line segment GH, it always passes through O.
Step 6: Now we have to repeat from step3 but this time taking C as a center and taking any radius (more than half of CD is recommended) draw two arcs, one on each side (top and bottom) of chord CD, naming these as E and F.
Step 7: With center as D, and taking the same radius as taken in the previous step, draw two arcs one on each side of the chord CD, cutting the previous arc E and F respectively.
Step8: Draw a straight-line segment EF, it always passes through O. Now it is clear that perpendicular bisectors of EF and GH intersect at point O, which is the center of the circle.
Hence, they are interested in the center of the circle.

Note: In the above solution we came across the terms like “chord” and “perpendicular bisector” where chord can be explained as the straight line whose both endpoints lie on the circle or points which lie on curve whereas line which cuts a line segment into two equal halves at \[{90^ \circ }\] for example in the above solution when AB and CD is bisected by the GH and EF at \[{90^ \circ }\].