Question

Draw a circle of radius $4.5$ cm. Draw two tangents to the circle so that the angle between the tangents is ${60^o}$.

Answer 1

Hint: We will draw a line segment of $4.5cm$ then will make a circle of radius $4.5cm$thereafter will make an angle ${90^o}$ at the point A. Further at point O we will make an angle ${120^o}$ and at the last we will make an angle ${60^o}$ at point D.


Complete step by step solution:
(i) Make a line segment $OA = 4.5cm$

(ii) Draw circle with centre $O$ and taking $OA = 4.5$ as a radius

(iii) At point A, make an angle of ${90^o}$

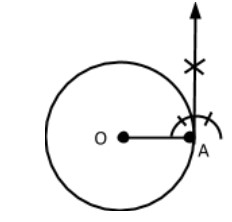
(iv) At point $O,$ make an angle of $\angle BOA = 120$ such that an arcs making an angle of $180 - 60 = {120^o}$

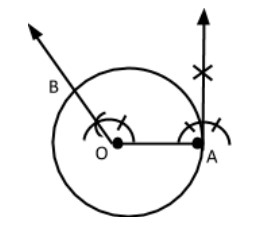
(v) When we make an angle ${120^o}$ at vertex $O$,then this ray intersects on the circle at point $B$.
(vi) At $B$, make an angle of ${90^o}$.

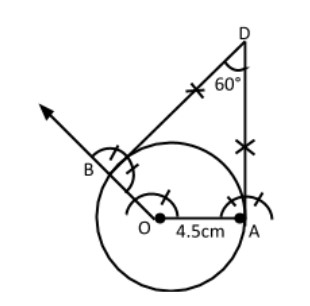
(vii) At $A\,\,and\,\,B$, draw two rays making an angle of ${90^o}$ at each point which meet each other at point $D$, outside the circle.
(viii) $AD$ and $BD$ are the required tangents which make an angle of ${60^o}$with each other at $D.$


Note: Students should draw angles carefully, angles have to be drawn to appropriate measure with the help of the right instruments