Question

Draw a circle of radius 3.5 cm and construct a chord of length 6cm in it. Measure the distance between the center and the chord.

Answer 1

Hint: General concepts of how to construct a circle when the radius of the circle is given will be required to solve questions of this type. The line drawn from the center of the circle to the midpoint of the chord will be a perpendicular bisector.

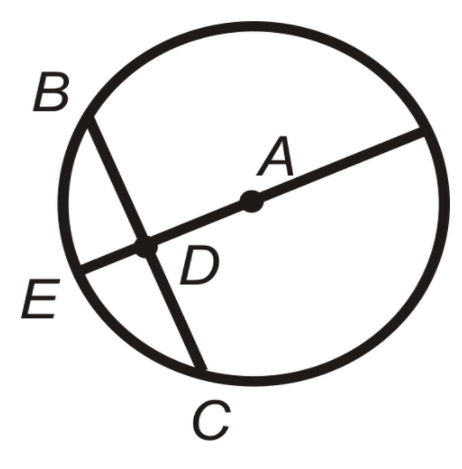
In the above figure, A is the center of the circle, BC is a chord of the circle. Now here is assumed that D is a midpoint to the chord BC then the line AE intersecting the chord at BC at D would be a perpendicular bisector, which means $\angle ADC=\angle ADB={{90}^{\circ }}$ and $BD=DC=\dfrac{BC}{2}$.

Complete step-by-step solution:
Firstly, here we need to draw a circle with a radius of 3.5 cm.

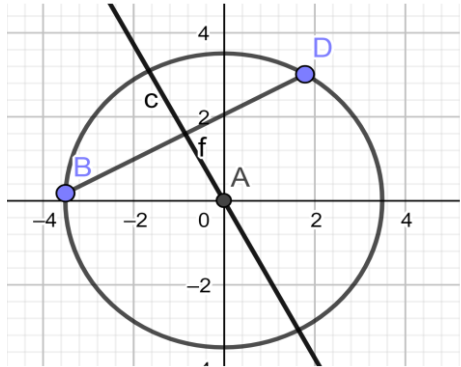
Let us name the center of the chord as shown in the above diagram as E.
So now, $\angle AED=\angle AEB={{90}^{\circ }}$ As the line AE would be the perpendicular bisector of the chord BD.
We know that the radius of the circle is 3.5cm. let us assume r = 3.5cm.
AD = AB = 3.5cm
AE is the bisector of the line segment BD
\[BE=ED=\dfrac{BD}{2}\]
As given in the question the length of chord BD is BD = 6cm
\[BE=ED=\dfrac{BD}{2}=\dfrac{6}{2}=3cm\]
ED = 3cm
 $\angle AED={{90}^{\circ }}$, $\Delta ADE$ would be a right angled triangle with two of its sides as ED = 3cm, AD = 3.5cm
Pythagoras theorem can be used as $\angle AED={{90}^{\circ }}$
From Pythagoras theorem,${{\left( AD \right)}^{2}}={{\left( ED \right)}^{2}}+{{\left( EA \right)}^{2}}$
Substituting the values of ED = 3cm and AD = 3.5cm we can obtain the value of EA
${{\left( AD \right)}^{2}}={{\left( ED \right)}^{2}}+{{\left( EA \right)}^{2}}$
$\Rightarrow {{\left( 3.5 \right)}^{2}}={{\left( 3 \right)}^{2}}+{{\left( EA \right)}^{2}}$
$\begin{align}
  &\Rightarrow {{\left( EA \right)}^{2}}={{\left( 3.5 \right)}^{2}}-{{\left( 3 \right)}^{2}} \\
 &\Rightarrow {{\left( EA \right)}^{2}}=12.25-9 \\
 &\Rightarrow {{\left( EA \right)}^{2}}=3.25 \\
 &\Rightarrow \left( EA \right)=\sqrt{3.25} \\
 &\Rightarrow \left( EA \right)=1.8027 \\
\end{align}$
EA = 1.8027cm
Therefore EA is the distance between the centre of the chord and centre of the circle, which is EA = 1.8027cm

Note: The important part of the question is to know that the line joining the center of the circle to the center of the chord would be a perpendicular bisector to the chord. Another way of solving this question is directly by constructing a circle with the given radius and then draw an arc with the given chord length then measure the distance.