Question

Draw a circle of diameter 7 cm and construct tangents at the ends of the diameter.

Answer 1

Hint: We will draw the circle using a compass. First, we will draw its diameter using a scale. Then, we will construct a perpendicular bisector at both ends of its diameter. These bisectors will be the tangents to the circle.

Formulas used:
 We will use the formula \[2\left( {{\rm{radius}}} \right) = {\rm{diameter}}\].
Complete step-by-step answer:
We know that the diameter of a circle is 2 times its radius.
Now, we will calculate the radius of the circle.
\[2r = 7\]
Dividing both side by 2, we get
\[\begin{array}{l} \Rightarrow r = \dfrac{7}{2}\\ \Rightarrow r = 3.5\end{array}\]
We have calculated that the radius of the circle is 3.5 cm
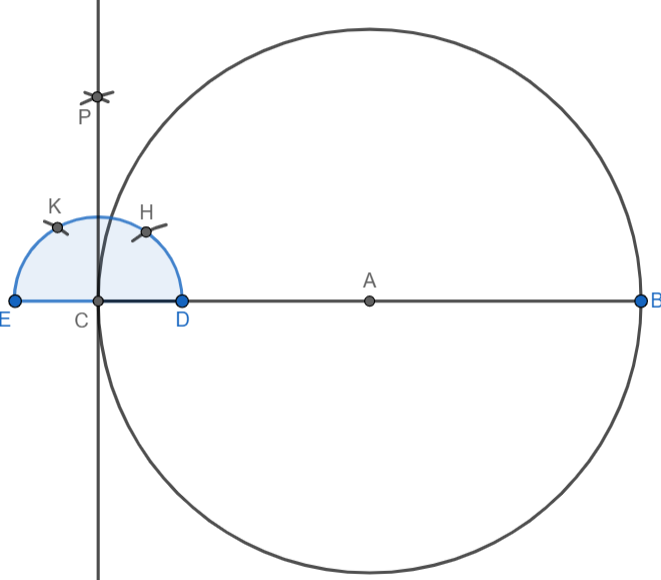
First, we will draw a circle of radius 3.5 cm. We will take a scale and open the compass 3.5 cm. We will choose a centre for the circle and construct it. We will also draw the diameter of the circle by making a line passing through its centre:

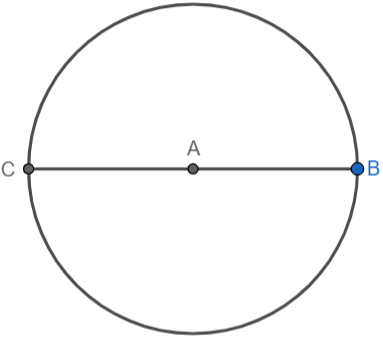
We know that tangents are perpendicular to the radius at the point of contact. We will construct right angles at points C and B. We will take C as the centre and construct a small semi-circle using a compass:

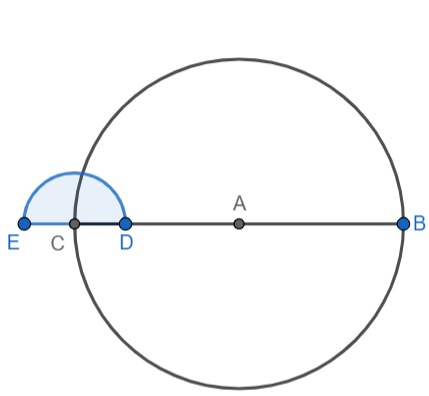
We will take point D as centre and keep the same radius used for drawing the semi-circle. We will draw an arc, intersecting the semicircle at point H. This arc will represent an angle of \[60^\circ \]. We will take point E as centre and keep the same radius used for drawing the semi-circle. We will draw an arc, intersecting the semicircle at point K. This arc will represent an angle of \[120^\circ \].

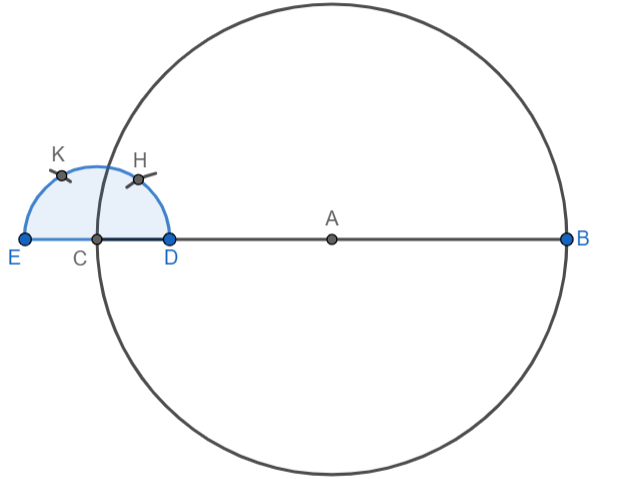
Taking the same radius, we will draw an arc with H as centre and an arc with K as centre. We will label the point of intersection of these arcs as P:

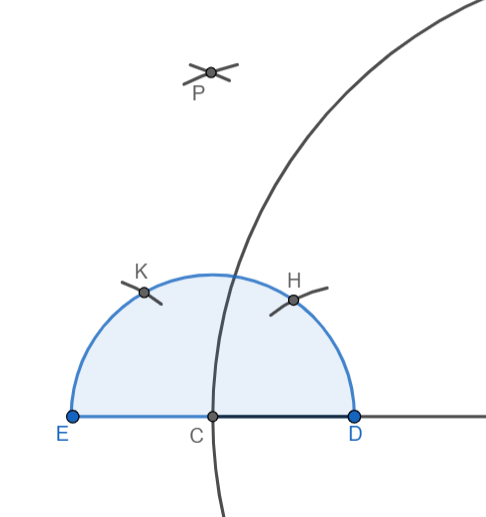
We will join points P and C and extend the line segment. This line will be the tangent to the circle at point C:

We will draw a tangent at point B using the same procedure as mentioned above:

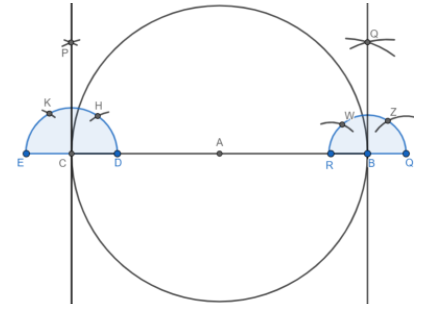
QB is the tangent to the circle at point B.

Note: We must be careful that the radius taken to construct angles of \[60^\circ \] and \[120^\circ \] should be the same as the radius taken to draw the semi-circle at the end of the diameter. Otherwise, we will not be able to construct the angle of the same measure and the tangent we have constructed will also be inaccurate.