Question

Draw a circle and divide it into 3 equal parts.

Answer 1

Hint: We will divide the circle into three parts by dividing it into 3 equal sectors of ${{120}^{\circ }}$ each. We are dividing circle into sectors of ${{120}^{\circ }}$ because a complete circle is of ${{360}^{\circ }}$ and to divide the circle into 3 equal parts, we will divide ${{360}^{\circ }}$ by 3, so we will get ${{120}^{\circ }}$.

Complete step-by-step answer:
It is given in the question that we have to draw a circle and divide it into 3 equal parts.
We know that a circle is equal to ${{360}^{\circ }}$. So, on dividing the circle into 3 equal parts, we get 3 equal sectors of ${{120}^{\circ }}$ as $\dfrac{{{360}^{\circ }}}{3}={{120}^{\circ }}$.
So, now we will divide a circle into 3 equal sectors of ${{120}^{\circ }}$ each. So, to do the same, we will follow a few steps as shown below.
Step1: We will take a random radius and then we will draw the circle.

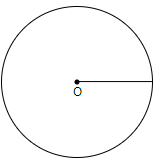
Step2: We will now draw ${{120}^{\circ }}$ angle. So, for that also, we will follow a few steps. We will use a compass to draw ${{120}^{\circ }}$.
So, first, taking any radius on the compass, we will draw an arc with the center as O.

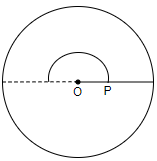
Then, with the same distance on the compass, we will place the compass at point P and then we will cut an arc on the existing arc. So, we get,

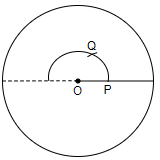
Now, with the same distance on the compass, we will place the compass at point Q, and then we will cut an arc on the existing arc. So, we get,

The point R obtained measures ${{120}^{\circ }}$ from point P in the anti-clockwise direction, so we get the angle ${{120}^{\circ }}$.

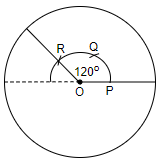
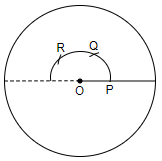
Step3: We will now draw another ${{120}^{\circ }}$, but this time, we will take the arc downwards. And we will follow step 2 again to draw ${{120}^{\circ }}$. So, we will get,

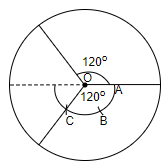
Step4: Since we have already measured two ${{120}^{\circ }}$, that is we get 2 equal sectors, so the angle in the reaming sector will also be ${{120}^{\circ }}$, so we will get,

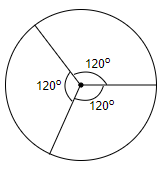
Thus, we have divided the circle into three equal parts, that is, three equal sectors of ${{120}^{\circ }}$ each.

Note: Many students divide the circle into three parts as any one of the follows.

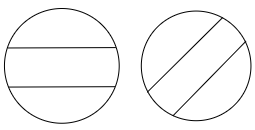
But this is not a correct method as the division by this method does not divide the circle equally. Also, there are high chances of errors, as it is a circular shaped figure. Thus, it is recommended that the students follow the correct method to solve this question. Also, the students must remember that the circle has the measure of $360˚\circ$ so to divide the circle to ‘n’ equal number of parts, we will write it as, $\dfrac{{{360}^{\circ }}}{n}$.