Question

How do you draw $45{}^\circ $ and $-45{}^\circ $ in standard position and then show that $\cos \left( -45{}^\circ \right)=\cos \left( 45{}^\circ \right)?$

Answer 1

Hint: We know that the initial side of the angle lies along the $x-$axis. When we draw a positive angle, we will start the rotation from the positive $x-$axis in the counterclockwise direction. When we draw a negative angle, we will start the rotation from the negative $x-$axis in the clockwise direction.

Complete step by step answer:
We are asked to draw the angle $45{}^\circ $ and $-45{}^\circ $ in the standard position.
As we can see, we need to draw a positive angle and a negative angle.
Let us consider the initial sides of the angles. We will locate the initial side along the $x-$axis.
When we draw a positive angle, we will start the rotation from the positive $x-$axis in the counterclockwise direction and when we draw a negative angle, we will start the rotation from the negative $x-$axis.
So, a graph containing $45{}^\circ $ and $-45{}^\circ $ angles in the standard position is given below:

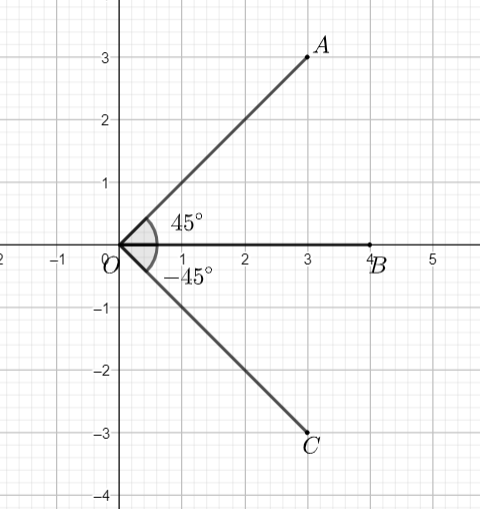
And now, we need to prove that $\cos \left( -45{}^\circ \right)=\cos 45{}^\circ .$
We know that the Cosine function is an even function.
We have learnt that all even functions satisfy the property given by: $f\left( -x \right)=f\left( x \right).$
Therefore, the Cosine function satisfies the property: $\cos \left( -x \right)=\cos \left( x \right).$
Hence, we have proved that $\cos \left( -45{}^\circ \right)=\cos 45{}^\circ .$

Note: We know that $\cos \left( -45{}^\circ \right)=\cos \left( 0{}^\circ -45{}^\circ \right).$ We will use the identity $\cos \left( x-y \right)=\cos x\cos y+\sin x\sin y.$ Then we will get $\cos \left( -45{}^\circ \right)=\cos \left( 0{}^\circ -45{}^\circ \right)=\cos 0{}^\circ \cos 45{}^\circ +\sin 0{}^\circ \sin 45{}^\circ .$ Also, we know that $\cos 0{}^\circ =1, \cos 45{}^\circ =\dfrac{1}{\sqrt{2}}, \sin 0{}^\circ =0$ and $\sin 45{}^\circ =\dfrac{1}{\sqrt{2}}.$ Now, we will get $\cos \left( -45{}^\circ \right)=\cos 0{}^\circ \cos 45{}^\circ +\sin 0{}^\circ \sin 45{}^\circ =1\times \dfrac{1}{\sqrt{2}}+0=\dfrac{1}{\sqrt{2}}=\cos 45{}^\circ .$ Remember that the Sine function is an odd function. So, it satisfies the property given by $f\left( -x \right)=-f\left( x \right).$