Question

What does the slope of the position-time graph indicate?

Answer 1

Hint: Let us first get some idea about graphs. A graph is a structure consisting of a set of items in which some pairs of the objects are in some way "connected" in mathematics, and more specifically in graph theory. Each of the connected pairs of vertices is termed an edge, and the objects correspond to mathematical abstractions called vertices (sometimes called nodes or points) (also called link or line). A graph is typically portrayed as a group of dots or circles for the vertices, linked by lines or curves for the edges, in diagrammatic form.

Complete step by step solution:
The velocity of an object is represented by the slope of a location graph. As a result, the value of the slope at a given moment shows the object's velocity at that time.

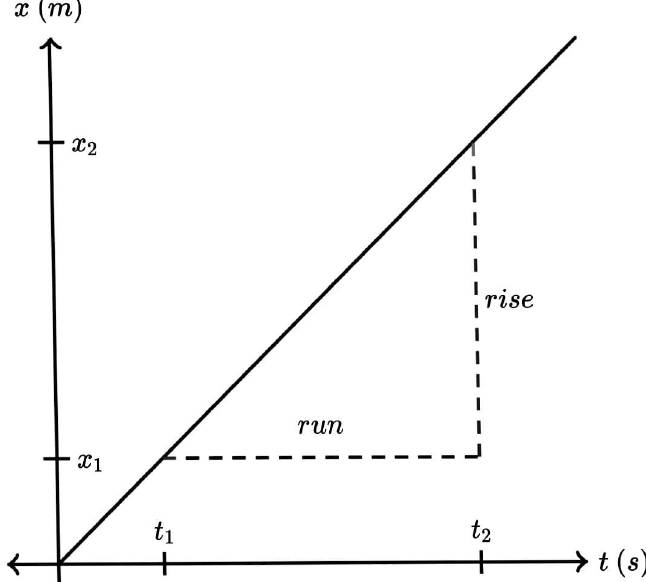
So, we can write from the above graph:
The slope of this position graph is: $Slope = \dfrac{{rise}}{{run}} = \dfrac{{{x_2} - {x_1}}}{{{t_2} - {t_1}}}$
The concept of velocity is the same as the definition of slope:
$v = \dfrac{{\vartriangle x}}{{\vartriangle t}} = \dfrac{{{x_2} - {x_1}}}{{{t_2} - {t_1}}}$. The slope of the position graph has to equal the velocity.
Another thing to remember is that the instantaneous velocity is determined by the slope of a position graph at a given point in time.

Note: You may get the average velocity between two places in time by calculating the average slope between them. The average velocity does not have to match the immediate velocity. If, on the other hand, the slope remains constant over time (i.e., the graph is a straight line segment), the instantaneous velocity equals the average velocity between any two places on the line segment.