Question

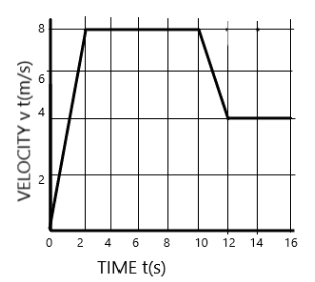
How far does the runner whose time-velocity graph is shown in the figure travel in 16 seconds

Answer 1

Hint: Area under the curve of a velocity - time graph (or time – velocity graph) is equal to the displacement covered. Split the velocity time graphs into simple shapes and calculate each of their areas, then add them together.

Formula used: In this solution we will be using the following formulae;
 $ {A_t} = \dfrac{1}{2}bh $ where $ {A_t} $ is the area of a triangle, $ b $ is the base of the triangle, and $ h $ is the height of the triangle.
 $ {A_r} = lb $ where $ {A_r} $ is the area of a rectangle, $ l $ is the length of the rectangle, and $ b $ is the breath of the rectangle.

Complete Step-by-Step solution
Generally, when a velocity time graph of an object is known, the area under the curve is the displacement of the object. Hence, to find how far the runner went, we shall calculate the area under each curve of the graph shown.
So be simpler, we split it into simple shapes. The first one being the triangle. The area under the triangle ABC is
 $ {A_t} = \dfrac{1}{2}2\left( 8 \right) $ since $ {A_t} = \dfrac{1}{2}bh $ where $ {A_t} $ is the area of a triangle, $ b $ is the base of the triangle, and $ h $ is the height of the triangle
 $ {A_{ABC}} = 8m $
For the rectangle / square CBDE we have
 $ {A_{CBDE}} = \left( {10 - 2} \right)\left( 8 \right) $ since $ {A_r} = lb $ where $ {A_r} $ is the area of a rectangle, $ l $ is the length of the rectangle, and $ b $ is the breath of the rectangle.
Then the triangle, DFG is
 $ {A_{DFG}} = \dfrac{1}{2}\left( {12 - 10} \right)\left( {8 - 4} \right) = 4{m^2} $
Rectangle EFGH,
 $ {A_{EFGH}} = \left( {12 - 10} \right)\left( 4 \right) = 8{m^2} $
Rectangle GHIJ
 $ {A_{GHIJ}} = \left( {16 - 12} \right)\left( 4 \right) = 16{m^2} $
To the total area under the curve is
 $ A = 8 + 4 + 8 + 16 = 36m $
Hence, the total displacement covered is 36 m.

Note
Although, it didn’t apply in this case, note that, the velocity time graphs shows gives total displacement, and hence when the velocity is negative, for total displacement, the area under (actually, it would be above the curve now) would be subtracted and not added.