Question

How does the graph of $y=-2{{x}^{2}}$ differ from $y=-2{{x}^{2}}-2$?

Answer 1

Hint: First we will draw the graph of the two parabolas. To do this, we need to change the given equation of parabola into their standard form given as: ${{\left( x-a \right)}^{2}}=4m\left( y-b \right)$. Here, (a, b) = vertex of parabola, (a, m + b) = focus and the parabola will open upward or downward according to the positive or negative value of m respectively. Finally, we will compare the graphs of the two parabolas and note the difference.

Complete step by step answer:
Here we have been provided with the two parabolas $y=-2{{x}^{2}}$ and $y=-2{{x}^{2}}-2$, we are asked to observe the difference between them by considering the plot of their graphs.
Now, to draw the graph of the parabolas we need to know its vertex, focus and concavity. To know these things we first convert them into their standard form given as: ${{\left( x-a \right)}^{2}}=4m\left( y-b \right)$. Here, we have (a, b) = vertex, (a, m + b) = focus and the concavity of the parabola will be opening upward or downward according to the positive or negative value of m respectively.
(1) Considering the parabola $y=-2{{x}^{2}}$ we have,
$\begin{align}
  & \Rightarrow -\dfrac{1}{2}y={{x}^{2}} \\
 & \Rightarrow {{\left( x-0 \right)}^{2}}=4\times \left( \dfrac{-1}{8} \right)\left( y-0 \right).............(i) \\
\end{align}$
Clearly, we have vertex = (0, 0), focus = $\left( 0,\dfrac{-1}{8} \right)$ and the parabola will be opening downwards.
(2) Considering the parabola $y=-2{{x}^{2}}-2$ we have,
\[\begin{align}
  & \Rightarrow -\dfrac{1}{2}y={{x}^{2}}+1 \\
 & \Rightarrow -\dfrac{1}{2}y-1={{x}^{2}} \\
 & \Rightarrow {{\left( x-0 \right)}^{2}}=4\times \left( \dfrac{-1}{8} \right)\left( y+2 \right).............(ii) \\
\end{align}\]
Clearly, we have vertex = (0, -2), focus = $\left( 0,\dfrac{-17}{8} \right)$ and the parabola will be opening downwards.
Therefore, the graph of the two parabolas can be plotted as:

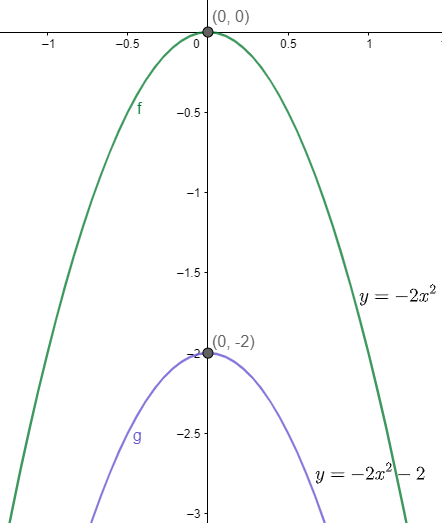
From the above graph we can notice that the vertex of the parabola $y=-2{{x}^{2}}-2$ is shifted 2 units downward as compared to the vertex of the parabola $y=-2{{x}^{2}}$. Also, the focus of the former is shifted 2 units downward as compared to the focus of the latter.

Note: In addition to the differences we have noticed in the two parabolas there is also a similarity between them. The concave nature of the parabola is the same in both the cases as they are opening downwards. We have another type of parabola given as ${{\left( y-a \right)}^{2}}=4m\left( x-b \right)$ that opens right or left according to the positive or negative values of m respectively.