Question

What does the area of an 'acceleration-displacement' graph represent?
A. Displacement
B. Velocity
C. $\dfrac{{{v^2} - {u^2}}}{2}$
D. $\dfrac{{v - u}}{2}$

Answer 1

Hint:We are given to find the area under the curve of an acceleration-displacement graph. For this, we have to use the method of integration to find the result. We have to consider velocity terms and change the time rate of change of displacement as velocity and hence find the solution.

Complete step by step answer:

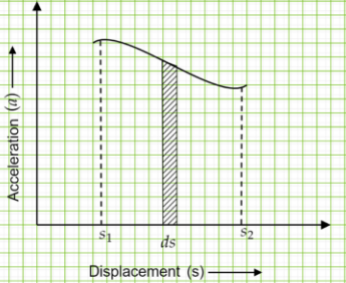
Let us consider a small strip of elements of displacement $s$ along the horizontal axis as $ds$. In order to find the area under the curve we have to integrate acceleration $a$ with respect to displacement element $ds$ from ${s_1}$ to ${s_2}$.
Thus, by the method of integration we find the area under the curve$ = \int_{{s_1}}^{{s_2}} {a.ds} - - - - \left( 1 \right)$

Let us consider velocity as $V$. Then we know, acceleration is defined as the time rate of change of velocity.
So, we can write $a = \dfrac{{dV}}{{dt}}$, again velocity can also be written as change in the rate of displacement $V = \dfrac{{ds}}{{dt}}$.
So, we can write equation $\left( 1 \right)$ as,
$\int_{{s_1}}^{{s_2}} {a.ds} = \int_{{s_1}}^{{s_2}} {\dfrac{{dV}}{{dt}}.ds} $
When we change $V = \dfrac{{ds}}{{dt}}$ then the limits will be changed from initial velocity $u$ to final velocity $v$. So, we get,
$\int_{{s_1}}^{{s_2}} {\dfrac{{ds}}{{dt}}.dV = \int_u^v {V.dV} } $
Integrating the equation we get,
$ \therefore \int_{{s_1}}^{{s_2}} {a.ds} = \left[ {\dfrac{{{V^2}}}{2}} \right]_u^v = \dfrac{{{v^2} - {u^2}}}{2}$

So, the correct option is C.

Note:It must be noted that in order to find the area of any curve which is not in regular shape we must use the limits of integration to find the answer. We can also take a strip from the vertical axis and integrate it with respect to displacement. The first derivative of displacement with respect to time is velocity and the second derivative of displacement with respect to time is acceleration.