Question

Does amplitude affect period?

Answer 1

Hint: Recall that the amplitude is defined as the maximum displacement of an object executing oscillatory motion. The amplitude is differentially dependent or independent on the period of oscillation based on the angle through which it moves away from the vertical. Remember that for large amplitudes, the pendulum tends to traverse through points of unstable equilibrium. To this end, deduce to what extent this would affect the pendulum’s oscillation period.

Complete answer:
Consider a pendulum executing oscillatory motion starting from A as shown in the figure.

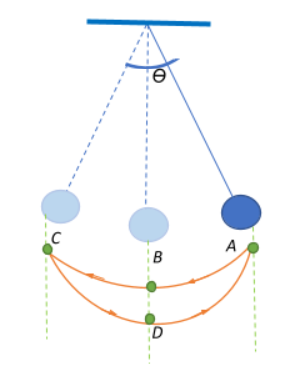
Let the pendulum execute one oscillation while going through ABCDA. The time taken to complete this oscillation is called the time period of the pendulum. Let the angular displacement amplitude of the pendulum be $\theta$. This is nothing but the maximum angle that the pendulum swings away from the vertical.
We know that the period of the pendulum’s swing depends on the length of the string and the local strength of gravity acting on it. But to a small extent, it also depends on $\theta$. If the amplitude is limited to small swings then the period of the pendulum will be:
$T = 2\pi\sqrt{\dfrac{l}{g}}$ for $\theta < < 1\;rad$ or $\theta < < 60^{\circ}$
Thus, for small swings the period of oscillation is approximately the same for all such swings, i.e., the period is independent of amplitude. This is called isochronism and is one of the reasons why pendulums are reliable time-keepers since even if successive swings are subject to change in amplitude, the pendulum would still take the same amount of time.
For larger amplitudes however, the period increases gradually with amplitude so it is no longer defined by the previous equation. The period increases asymptotically (to infinity) as $\theta \rightarrow \pi\;rad \;(180^{\circ})$ because $\theta = \pi$ is an unstable equilibrium point for the pendulum.

Note:
Note that the difference between the true period given (given by the equation of period for larger amplitudes, that we have not discussed here) and the period for small swings is called the circular error. A typical grandfather clock has a swing of $6^{\circ}$ which means it has an amplitude of $3^{\circ}\;(0.05\;rad)$. The difference between the true period and the small amplitude approximation amounts to a circular error of about $15\;s$ a day.
In any case, the period of a pendulum does not depend on its mass or its initial displacement.