Question

What does a cross product of $0$ mean?

Answer 1

Hint: We will first understand the meaning of cross product and how it is used. We will use the definition that the cross product of two vectors is given by the formula
$\overrightarrow A \times \overrightarrow B = \left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right|\sin \theta $ , where $\theta $ is the angle between the two vectors.

Complete step by step solution:
As we know, the cross product is the binary operation on two vectors in three-dimensional space. It shows us two vectors that are parallel to each other.
We know that the cross product meaning relies on the concept of vectors i.e. it is related with the product of vectors such as
$\overrightarrow A \times \overrightarrow B $ .
Cross Product Formula:
If $\theta $ is the angle between the given vectors, then the formula is denoted by
$\overrightarrow A \times \overrightarrow B = \left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right|\sin \theta \,\,\hat n$ , where $\left| {\overrightarrow A } \right| = $ length of vector A
 $\left| {\overrightarrow B } \right| = $ length of vector B
$\theta = $Angle between A and B
And, $n = $ unit vector perpendicular to the plane,
This can be written as the cross product of two vectors is magnitude-wise equal to the product of their magnitude with their sides of that angle between them .
So if we have
$\sin \theta = 0$, then according to formula the result will be
 $\left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right| \times 0 = 0$ .
So if the cross product of two vectors is zero then the two vectors are parallel to each other or the angle between them is $0$.
Hence If the two vectors are in the same direction, then the angle between them $\theta $ is
$0$.
So the resultant vector will be the zero vector.

Note:
We can understand the cross product formula with the example.
Let us draw a parallelogram.

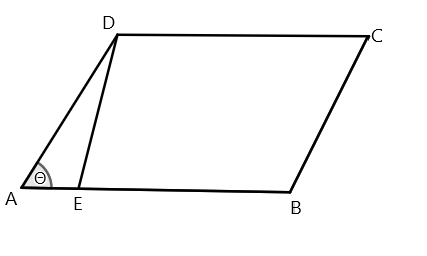
We know the area of the parallelogram is base $ \times $ height. Here Base is $AB$ and height $ = DE$ .
We know that the cross product of two dimensional figures gives us a vector which is equal to the area enclosed by the parallelogram between two vectors or sides.
Here we have $\left| {\overrightarrow A } \right| = AB$ and $\left| {\overrightarrow B } \right| = DE$
So by applying the formula here we can say that the area is
 $AB \times DE \times \sin \theta $