Question

Distance of the center of mass of a solid uniform cone from its vertex is ${{z}_{0}}$. If the radius of its base is R and its height is ‘h’ then ${{z}_{0}}$ is equal to:
$\begin{align}
  & \text{A}\text{. }\dfrac{{{h}^{2}}}{4R} \\
 & \text{B}\text{. }\dfrac{3h}{4} \\
 & \text{C}\text{. }\dfrac{5h}{4} \\
 & \text{D}\text{. }\dfrac{3{{h}^{2}}}{8R} \\
\end{align}$

Answer 1

- Hint: The center of a solid body can be calculated by taking a suitable cross-section in the body, applying it in the center of mass formula for continuous bodies and integrating it throughout to get the center of mass.

Complete step-by-step solution -
In this question we are given a solid uniform cone of radius R and height h, we need to find the center of mass from the vertex. Given below is a rough diagram of the solid cone.

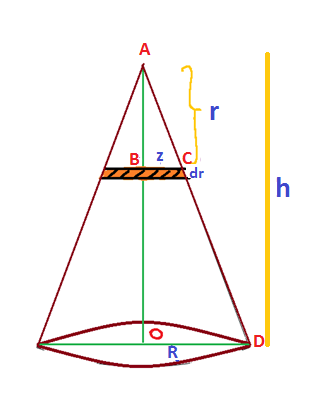
We will consider a small circular cross-section of radius ‘z’ and thickness ‘dr’ from a distance ‘r’ from the vertex of the solid cone.
Consider two triangles ABC and AOD. These triangles are similar triangles, so we can write,
$\dfrac{\text{AB}}{\text{AO}}=\dfrac{\text{BC}}{\text{OD}}$
Which can be expressed as,
$\dfrac{\text{r}}{\text{h}}=\dfrac{\text{z}}{\text{R}}$ …… equation (1)
The volume of the small volume element considered is given by, $dV=\pi {{z}^{2}}dr$, which can be written in terms of r using equation (1). So we get,
$dV=\dfrac{\pi {{R}^{2}}{{r}^{2}}}{{{h}^{2}}}dr$ …. equation (2)
The center of mass for continuous mass distribution is given by the formula,
$\text{C}\text{.M}=\dfrac{1}{\text{M}}\int{rdm}$
Where,
M is the mass of the circular cone.
dm is the mass of the small element we are considering.
The small mass dm can be written as $dm=\rho dV$. $\rho $ is the volume density of the solid cone.
Therefore, we can write
\[\begin{align}
  & \text{C}\text{.M}=\dfrac{1}{\text{M}}\int{r\rho \dfrac{\pi {{R}^{2}}{{r}^{2}}}{{{h}^{2}}}dr} \\
 & C.M=\dfrac{\pi {{R}^{2}}\rho }{M{{h}^{2}}}\int{{{r}^{3}}dr} \\
\end{align}\]
The limits of the integration are from zero to h, so we can write,
$C.M=\dfrac{\pi {{R}^{2}}\rho }{M{{h}^{2}}}\int\limits_{0}^{h}{{{r}^{3}}dr}$
Integrating and applying the limits we will get,
$C.M=\dfrac{\rho {{R}^{2}}\pi {{h}^{2}}}{4M}$

Substituting M as $\text{M}=\text{ }\!\!\rho\!\!\text{ V}=\text{ }\!\!\rho\!\!\text{ (1/3 }\!\!\pi\!\!\text{ }{{\text{R}}^{\text{2}}}\text{h)}$, we can write
$\text{C}\text{.M}=\dfrac{3h}{4}$
So the answer to the question is option (B) $\dfrac{3h}{4}$

Note: The distance to the center of mass from point O is $\dfrac{h}{4}$.
The center of mass of the cone will always lie on its axis due to symmetry.
The center of mass of a distribution of mass in space (sometimes referred to as the balance point) is the unique point where the weighted relative position of the distributed mass sums to zero. This is the point to which a force may be applied to cause a linear acceleration without an angular acceleration.