Question

How is the distance between the Earth and the Moon calculated?

Answer 1

Hint: The distance between the Earth and the Moon can be measured using the Parallax method. A parallax is defined as the difference in the apparent position of an object, when viewed along two different lines of sight. It is measured by the angle or semi-angle of inclination between the two lines of sight. Therefore, while measuring shorter distances the angle of inclination is large and while measuring the distance of a far off distant object, the angle of inclination is very small.

Complete answer:
Let us first define some useful terms that are to be used:
D: the distance between the Earth and the moon.
b: the distance between the two points on Earth.
$\theta $ : the parallax angle.
Now, let us visualize the problem using the following diagram:

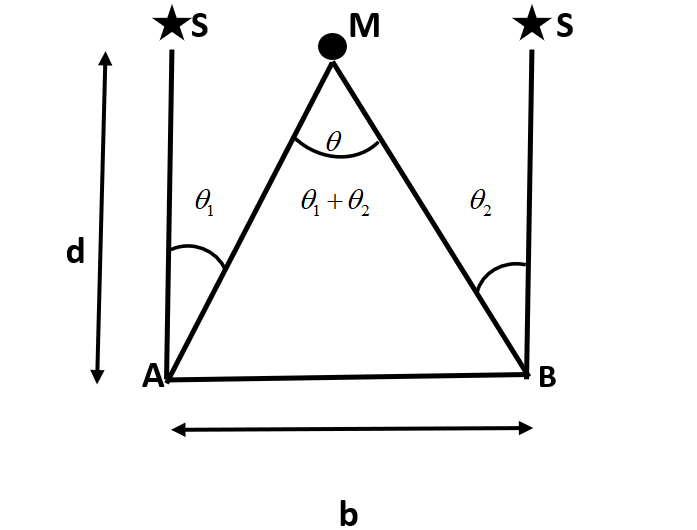
Here, we use a star S as reference. As it is too far away from the earth, we measure the angle that it makes, along the two different lines of sight.
Here,
AM and BM are the distance of the moon (M) from Earth, and
AB is the distance between the two points.
Thus, the whole set-up can be considered a part of a circle whose arc is AB with center M with the arc subtending an angle of ${{\theta }_{1}}+{{\theta }_{2}}$ at the center.
Therefore, for the arc we can write:
$\begin{align}
  & \Rightarrow AM({{\theta }_{1}}+{{\theta }_{2}})=AB \\
 & \Rightarrow D({{\theta }_{1}}+{{\theta }_{2}})=b \\
 & \Rightarrow D=\dfrac{b}{{{\theta }_{1}}+{{\theta }_{2}}} \\
\end{align}$
Where,
$\Rightarrow {{\theta }_{1}}+{{\theta }_{2}}=\theta $ is the parallax angle.
Hence, the distance of the Moon from the Earth is calculated to be $\dfrac{b}{{{\theta }_{1}}+{{\theta }_{2}}}$ .

Note:
While using parallax method for distant objects, the point of references on Earth should be considerably apart so that we get a measurable a parallax angle as small angles are harder to measure. The distance of the moon from the Earth can be calculated using the principle of Lunar Eclipse also which uses the concept of similar triangles.